题目内容
20．已知A={（x，y）||x|≤1，|y|≤1}，B是曲线$y=\sqrt{1-{{（{x-1}）}^2}}$围成的封闭区域，若向区域A上随机投一点P，则点P落入区域B的概率为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{16}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{8}$ |
分析 作出不等式组对应的平面区域，求出对应区域的面积，利用几何概型的概率公式进行计算即可．
解答 
解：作出不等式组对应的区域，则结合A对应正方形ABCD，面积S=2×2=4，
是曲线$y=\sqrt{1-{{（{x-1}）}^2}}$围成的封闭区域在正方形内为圆的$\frac{1}{4}$，对应的面积S=$\frac{1}{4}$×π×12=$\frac{π}{4}$，
则向区域A上随机投一点P，则点P落入区域B的概率P=$\frac{\frac{π}{4}}{4}$=$\frac{π}{16}$，
故选：B
点评 本题主要考查几何概型的概率的计算，作出对应的区域，求出对应的面积，利用几何概型的概率公式是解决本题的关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
10．若平面α，β的法向量分别为$\overrightarrow{n_1}$=（2，-3，5），$\overrightarrow{n_2}$=（-3，1，2），则（ ）
| A． | α∥β | B． | α⊥β | C． | α，β相交但不垂直 | D． | 以上均不正确 |
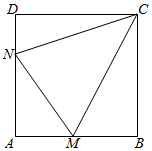如图所示，某村积极开展“美丽乡村•生态家园”建设，现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园，给村民休闲健身提供去处．点M，N分别在边AB，AD上．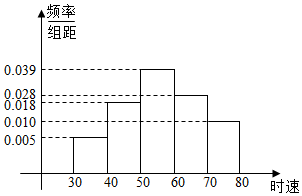
为检验寒假学生自主学生的效果，级部对某班50名学生各科的检测成绩进行了统计，下面是物理成绩的频率分布直方图，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．