题目内容
12.若虚数z=(a-1)+ai(a∈R)的模为1,则a=1.分析 利用复数模的计算公式、虚数的定义即可得出.
解答 解:∵虚数z=(a-1)+ai(a∈R)的模为1,
∴$\sqrt{(a-1)^{2}+{a}^{2}}$=1,a≠0,
化为a2-a=0,解得a=1.
故答案为:1.
点评 本题考查了复数模的计算公式、虚数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
3.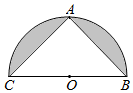 如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )
如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )
 如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )
如图,已知半径为2的半圆中,BC为直径,O为圆心,点A在半圆弧上,且AB=AC,则图中阴影部分绕直线BC旋转一周所形成的几何体的体积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | 16π | D. | 32π |
20.已知A={(x,y)||x|≤1,|y|≤1},B是曲线$y=\sqrt{1-{{({x-1})}^2}}$围成的封闭区域,若向区域A上随机投一点P,则点P落入区域B的概率为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
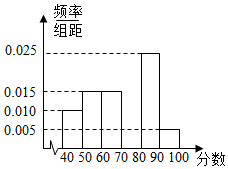 某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: 如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中用X表示.
如图茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中用X表示.