题目内容
10.函数f(x)=$\frac{{2}^{x}-3}{{2}^{x}+3}$的值域为(-1,1).分析 由2x>0,求得2x+3的范围,取倒数求得$\frac{1}{{2}^{x}+3}$的范围,两边同时乘以-1,得到$-\frac{1}{{2}^{x}+3}$的范围,进一步求得函数的值域.
解答 解:f(x)=$\frac{{2}^{x}-3}{{2}^{x}+3}$=$\frac{{2}^{x}+3-6}{{2}^{x}+3}=1-\frac{6}{{2}^{x}+3}$,
∵2x>0,
∴2x+3>3,
则0$<\frac{1}{{2}^{x}+3}<\frac{1}{3}$,
∴$-\frac{1}{3}<-\frac{1}{{2}^{x}+3}<0$,
则-2$<-\frac{6}{{2}^{x}+3}<0$,
∴f(x)∈(-1,1).
故答案为:(-1,1).
点评 本题考查函数的值域,体现了极限思想方法的运用,是中档题.

练习册系列答案
相关题目
20.已知A={(x,y)||x|≤1,|y|≤1},B是曲线$y=\sqrt{1-{{({x-1})}^2}}$围成的封闭区域,若向区域A上随机投一点P,则点P落入区域B的概率为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
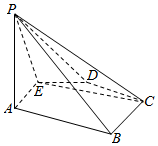 如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.
如图所示,已知在五棱锥P-ABCDE底面ABCDE为凸五边形,AE=DC=2,AB=BC=3,DE=1,∠EAB=∠BCD=∠CDE=∠DEA=120°,F为AE上的点,且AF=$\frac{3}{2}$,平面PAE与底面ABCDE垂直.