题目内容
10.若平面α,β的法向量分别为$\overrightarrow{n_1}$=(2,-3,5),$\overrightarrow{n_2}$=(-3,1,2),则( )| A. | α∥β | B. | α⊥β | C. | α,β相交但不垂直 | D. | 以上均不正确 |
分析 由法向量不平行且不垂直可判.
解答 解:由题意可得平面α,β的法向量分别为$\overrightarrow{n_1}$=(2,-3,5),$\overrightarrow{n_2}$=(-3,1,2),
∵$\overrightarrow{{n}_{1}}$和$\overrightarrow{{n}_{2}}$不平行,∵平面α和β不平行;
又$\overrightarrow{{n}_{1}}$•$\overrightarrow{{n}_{2}}$=-6-3+10=1≠0,∴平面α和β不垂直,
故选:C.
点评 本题考查平面的法向量,涉及平面平行和垂直的判定,属基础题.

练习册系列答案
相关题目
20.已知抛物线y=4ax2,则其准线方程是( )
| A. | y=-$\frac{1}{16a}$ | B. | x=-a | C. | y=±$\frac{1}{16a}$ | D. | x=±a |
5.在等差数列{an}中,a1=1,公差d=2,则a8等于( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
19.已知角α的顶点在原点,始边与x轴的非负半轴重合,终边交以原点为圆心的单位圆于点A,将角α的终边按逆时针方向旋转$\frac{π}{6}$后交此单位圆于点B,记A(x1,y1),B(x2,y2),若A(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),则x2的值为( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
20.已知A={(x,y)||x|≤1,|y|≤1},B是曲线$y=\sqrt{1-{{({x-1})}^2}}$围成的封闭区域,若向区域A上随机投一点P,则点P落入区域B的概率为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{8}$ |
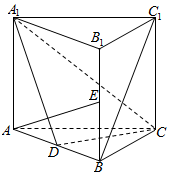 如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
如图,直三棱柱ABC-A1B1C1中,D、E分别是AB、BB1的中点,AB=$\sqrt{2}$,AA1=AC=CB=1.
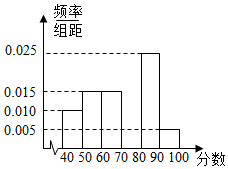 某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩分成六段[40,50),[50,60)…[90,100]后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: