题目内容
2.将一枚质地均匀的硬币连续抛掷n次,事件“至少有一次正面向上”的概率为$p({p≥\frac{15}{16}})$,则n的最小值为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 利用对立事件及n次独立重复试验中事件A恰好发生k次的概率计算公式得到p=1-($\frac{1}{2}$)n$≥\frac{15}{16}$,由此能求出n的最小值.
解答 解:将一枚质地均匀的硬币连续抛掷n次,
事件“至少有一次正面向上”的概率为$p({p≥\frac{15}{16}})$,
∴p=1-($\frac{1}{2}$)n$≥\frac{15}{16}$,
∴($\frac{1}{2}$)n≤$\frac{1}{16}$.
∴n的最小值为4.
故选:A.
点评 本题考查对立事件及n次独立重复试验中事件A恰好发生k次的概率计算公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
13.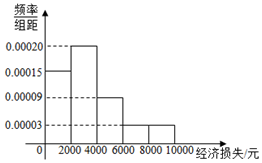 2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.
2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.
(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表所示,在表格空白处填写正确数字,并说明能否在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关?
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列,期望E(ξ)和方差D(ξ).
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
 2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.
2016年10月21日,台风“海马”导致江苏、福建、广东3省11市51个县(市、区)189.9万人受灾,某调查小组调查了受灾某小区的100户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出频率分布直方图.(Ⅰ)台风后居委会号召小区居民为台风重灾区捐款,小张调查的100户居民捐款情况如表所示,在表格空白处填写正确数字,并说明能否在犯错误的概率不超过0.05的前提下认为捐款数额超过或不超过500元和自身经济损失是否超过4000元有关?
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量受灾居民中,采用随机抽样的方法每次抽取1户居民,抽取3次,记被抽取的3户居民中自身经济损失超过4000元的人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列,期望E(ξ)和方差D(ξ).
| 经济损失不超过4000元 | 经济损失超过4000元 | 总计 | |
| 捐款超过500元 | 60 | ||
| 捐款不超过500元 | 10 | ||
| 总计 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
14.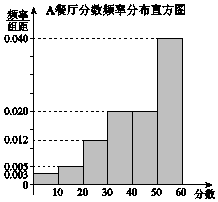 某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
定义学生对餐厅评价的“满意度指数”如下:
(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
 某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:| B餐厅分数频数分布表 | |
| 分数区间 | 频数 |
| [0,10) | 2 |
| [10,20) | 3 |
| [20,30) | 5 |
| [30,40) | 15 |
| [40,50) | 40 |
| [50,60] | 35 |
| 分数 | [0,30) | [30,50) | [50,60] |
| 满意度指数 | 0 | 1 | 2 |
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
11.若集合A={x|x-x2>0},B={x|(x+1)(m-x)>0},则“m>1”是“A∩B≠∅”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
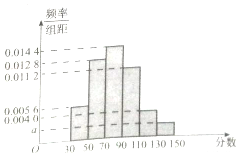 某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)
某市高二年级学生进行数学竞赛,竞赛分为初赛和决赛,规定成绩在110分及110分以上的学生进入决赛,110分以下的学生则被淘汰,现随机抽取500名学生的初赛成绩按[30,50),[50,70),[70,90),[90,110),[110,130),[130,150]做成频率副本直方图,如图所示:(假设成绩在频率分布直方图中各段是均匀分布的)