题目内容
如图,在四棱锥P ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=
ABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=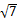 ,PA=
,PA=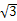 ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点.
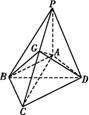
(1)证明:BD⊥平面APC;
(2)若G为PC的中点,求DG与平面APC所成的角的正切值;
(3)若G满足PC⊥平面BGD,求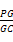 的值.
的值.
(1)证明:设点O为AC,BD的交点.
由AB=BC,AD=CD,得BD是线段AC的中垂线,
所以O为AC的中点,BD⊥AC.
又因为PA⊥平面ABCD,BD⊂平面ABCD,
所以PA⊥BD,所以BD⊥平面APC.
(2)解:连接OG.
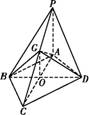
由(1)可知,OD⊥平面APC,
则DG在平面APC内的射影为OG,
所以∠OGD是DG与平面APC所成的角.
由题意得OG= PA=
PA=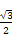 .
.
在△ABC中,
AC=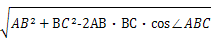
=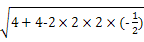
=2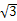 ,
,
所以OC= AC=
AC=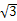 .
.
在直角△OCD中,OD=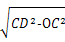 =
=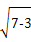 =2.
=2.
在直角△OGD中,tan∠OGD=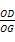 =
=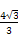 .
.
所以DG与平面APC所成的角的正切值为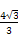 .
.
(3)解:因为PC⊥平面BGD,OG⊂平面BGD,
所以PC⊥OG.
在直角△PAC中,PC=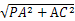 =
=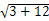 =
=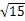 ,
,
所以GC=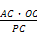 =
=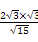 =
=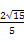 .
.
从而PG=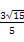 ,
,
所以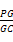 =
= .
.

练习册系列答案
相关题目
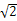 的等腰直角三角形,则该三棱锥的四个面的面积中最大的是 .
的等腰直角三角形,则该三棱锥的四个面的面积中最大的是 . 
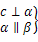 ⇒c⊥β
⇒c⊥β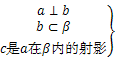 ⇒b⊥c
⇒b⊥c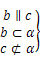 ⇒c∥α
⇒c∥α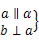 ⇒b⊥α
⇒b⊥α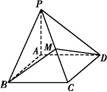
 (B)-
(B)- ,
, ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH的中点,PA=AC=2,BC=1.
ABC中,PA⊥底面ABC,AC⊥BC,H为PC的中点,M为AH的中点,PA=AC=2,BC=1.
 =λ,MN∥平面ABC,求实数λ的值.
=λ,MN∥平面ABC,求实数λ的值. -
- <
< 成立,则a,b应满足( )
成立,则a,b应满足( )