题目内容
16.已知直线y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A,B两点,且OA⊥OB(O为坐标原点),若椭圆的离心率e∈[$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$],则a的最大值为$\frac{\sqrt{3}}{2}$.分析 将直线方程代入椭圆方程,由韦达定理,向量数量积的坐标运算,求得2a2=1+$\frac{1}{1-{e}^{2}}$,由离心率的取值范围,即可求得a的最大值.
解答 解:设A(x1,y1)、B(x2,y2),
由$\left\{\begin{array}{l}{y=-x+1}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,消去y,可得(a2+b2)x2-2a2x+a2(1-b2)=0,
∴则x1+x2=$\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}$,x1x2=$\frac{{a}^{2}(1-{b}^{2})}{{a}^{2}+{b}^{2}}$,
由△=(-2a2)2-4a2(a2+b2)(1-b2)>0,整理得a2+b2>1.
∴y1y2=(-x1+1)(-x2+1)=x1x2-(x1+x2)+1.
∵OA⊥OB(其中O为坐标原点),可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=0
∴x1x2+y1y2=0,即x1x2+(-x1+1)(-x2+1)=0,化简得2x1x2-(x1+x2)+1=0.
∴2•$\frac{{a}^{2}(1-{b}^{2})}{{a}^{2}+{b}^{2}}$-$\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}$+1=0.整理得a2+b2-2a2b2=0.
∵b2=a2-c2=a2-a2e2,
∴代入上式,化简得2a2=1+$\frac{1}{1-{e}^{2}}$,
∴a2=$\frac{1}{2}$(1+$\frac{1}{1-{e}^{2}}$).
∵e∈[$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$],平方得$\frac{1}{4}$≤e2≤$\frac{3}{4}$,
∴$\frac{1}{4}$≤1-e2≤$\frac{3}{4}$,可得 $\frac{4}{3}$≤$\frac{1}{1-{e}^{2}}$≤4,
因此$\frac{7}{3}$≤2a2=1+$\frac{1}{1-{e}^{2}}$≤5,$\frac{7}{6}$≤a2≤$\frac{5}{2}$,可得a2的最大值为$\frac{5}{2}$,
满足条件a2+b2>1,
∴当椭圆的离心率e=$\frac{\sqrt{3}}{2}$时,a的最大值为$\frac{\sqrt{10}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | -3 | C. | 1 | D. | 3 |
 ,若函数
,若函数 有
有 个零点,则实数
个零点,则实数 的值为
的值为 B.
B.  C.
C.  D.
D. 
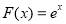 满足
满足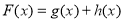 ,且
,且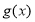 ,
,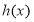 分别是
分别是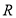 上的偶函数和奇函数,若
上的偶函数和奇函数,若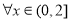 使得不等式
使得不等式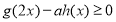 恒成立,则实数
恒成立,则实数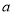 的取值范围是( )
的取值范围是( )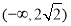 B.
B.
 D.
D.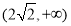
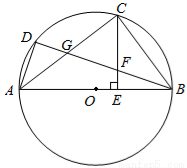
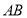 为圆
为圆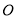 的直径,
的直径,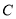 ,
,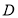 是圆
是圆 上的两个点,
上的两个点,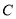 是劣弧
是劣弧 的中点,
的中点,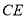 ⊥
⊥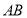 于
于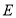 ,
,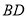 交
交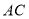 于
于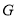 ,交
,交 于
于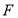 .
.
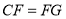 ;
;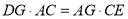 .
.