题目内容
已知PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上任意一点，过A点作AE⊥PC于点E，求证：AE⊥平面PBC.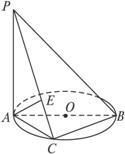
证明:∵PA⊥平面ABC，∴PA⊥BC.
又∵AB是⊙O的直径，
∴BC⊥AC.
而PC∩AC=C，
∴BC⊥平面PAC.
又∵AE在平面PAC内，
∴BC⊥AE.
∵PC⊥AE，且PC∩BC=C，
∴AE⊥平面PBC.
练习册系列答案
相关题目
题目内容
已知PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上任意一点，过A点作AE⊥PC于点E，求证：AE⊥平面PBC.
证明:∵PA⊥平面ABC，∴PA⊥BC.
又∵AB是⊙O的直径，
∴BC⊥AC.
而PC∩AC=C，
∴BC⊥平面PAC.
又∵AE在平面PAC内，
∴BC⊥AE.
∵PC⊥AE，且PC∩BC=C，
∴AE⊥平面PBC.
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且PA=AC=BC，E，F分别为PC，PB中点．
11、已知PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上任意一点，过A点作AE⊥PC于点E，求证：AE⊥平面PBC．
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点．F为PB中点．
（2013•韶关一模）如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=4，C是⊙O上一点，且PA=AC=BC，
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点，F为PB中点．