题目内容
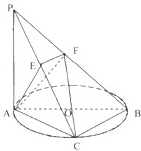 (2013•韶关一模)如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=4,C是⊙O上一点,且PA=AC=BC,
(2013•韶关一模)如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=4,C是⊙O上一点,且PA=AC=BC,| PE |
| PC |
| PF |
| PB |
(1)求证:EF∥面ABC;
(2)求证:EF⊥AE;
(3)当λ=
| 1 |
| 2 |
分析:(1)利用线线平行证明线面平行即可;
(2)先根据线面垂直的判定定理证明线面垂直,再根据线面垂直的性质证明线线垂直;
(3)利用三棱锥的换底性与棱锥的体积公式求解即可.
(2)先根据线面垂直的判定定理证明线面垂直,再根据线面垂直的性质证明线线垂直;
(3)利用三棱锥的换底性与棱锥的体积公式求解即可.
解答:解:(1)证明:在三角形PBC中,∵
=
=λ
∴EF∥BC,又BC?面ABC,EF?面ABC,
∴EF∥面ABC
(2)
⇒BC⊥PA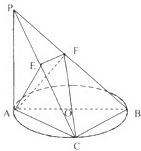
又∵AB是⊙O的直径,∴BC⊥AC,
∴BC⊥面PAC.
∵EF∥BC BC⊥面PAC,∴EF⊥面PAC
∵AE?面PAC,
∴EF⊥AE.
(3)∵在Rt△ABC中,AB=4∴PA=AC=BC=2
当λ=
时,E是PC中点.F为PB中点∴EF=
BC=
S△EAC=
S△PAC=
×
PA•AC=
×
×2
×2
=2,
∵EF⊥面PAC
∴VA-CEF=VF-ACE=
×S△ACE×EF=
×2×
=
.
| PE |
| PC |
| PF |
| PB |
∴EF∥BC,又BC?面ABC,EF?面ABC,
∴EF∥面ABC
(2)
|

又∵AB是⊙O的直径,∴BC⊥AC,
∴BC⊥面PAC.
∵EF∥BC BC⊥面PAC,∴EF⊥面PAC
∵AE?面PAC,
∴EF⊥AE.
(3)∵在Rt△ABC中,AB=4∴PA=AC=BC=2
| 2 |
当λ=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∵EF⊥面PAC
∴VA-CEF=VF-ACE=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
点评:本题考查线面平行的判定、线面垂直的性质及棱锥的体积计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•韶关一模)如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=CA=2,点E是PC的中点.
(2013•韶关一模)如图,三棱锥P-ABC中,PB⊥底面ABC于B,∠BCA=90°,PB=CA=2,点E是PC的中点.