题目内容
 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.F为PB中点.
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点.F为PB中点.(1)求证:EF∥面ABC;
(2)求证:EF⊥面PAC;
(3)求三棱锥B-PAC的体积.
分析:(1)在三角形PBC中,由E是PC中点,F为PB中点,知EF∥BC,由此能够证明EF∥面ABC.
(2)由PA⊥平面ABC,BC?平面ABC,知BC⊥PA,再由AB是⊙O的直径,知BC⊥AC,故BC⊥面PAC,由此能够证明EF⊥面PAC.
(3)因为PA⊥⊙O所在的平面,AC是PC在面ABC内的射影,所以∠PCA即为PC与面ABC所成角,故∠PCA=45°,PA=AC.由此能够求出三棱锥B-PAC的体积.
(2)由PA⊥平面ABC,BC?平面ABC,知BC⊥PA,再由AB是⊙O的直径,知BC⊥AC,故BC⊥面PAC,由此能够证明EF⊥面PAC.
(3)因为PA⊥⊙O所在的平面,AC是PC在面ABC内的射影,所以∠PCA即为PC与面ABC所成角,故∠PCA=45°,PA=AC.由此能够求出三棱锥B-PAC的体积.
解答:(1)证明:在三角形PBC中,
∵E是PC中点,F为PB中点,
∴EF∥BC,BC?面ABC,EF?面ABC,
∴EF∥面ABC.
(2)证明:∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA.
又∵AB是⊙O的直径,∴BC⊥AC,
∴BC⊥面PAC
∵EF∥BC,BC⊥面PAC,
∴EF⊥面PAC.
(3)解:∵PA⊥⊙O所在的平面,AC是PC在面ABC内的射影,
∴∠PCA即为PC与面ABC所成角,
∴∠PCA=45°,PA=AC,
在Rt△ABC中,E是PC中点,
∠BAC=
,AC=BC=
,
∴三棱锥B-PAC的体积VB-PAC=VP-ABC=
S△ABCPA=
.
∵E是PC中点,F为PB中点,
∴EF∥BC,BC?面ABC,EF?面ABC,
∴EF∥面ABC.
(2)证明:∵PA⊥平面ABC,BC?平面ABC,∴BC⊥PA.
又∵AB是⊙O的直径,∴BC⊥AC,
∴BC⊥面PAC
∵EF∥BC,BC⊥面PAC,
∴EF⊥面PAC.
(3)解:∵PA⊥⊙O所在的平面,AC是PC在面ABC内的射影,
∴∠PCA即为PC与面ABC所成角,
∴∠PCA=45°,PA=AC,
在Rt△ABC中,E是PC中点,
∠BAC=
| π |
| 4 |
| 2 |
∴三棱锥B-PAC的体积VB-PAC=VP-ABC=
| 1 |
| 3 |
| ||
| 3 |
点评:本题考查直线与平面平行的证明,考查直线与平面垂直的证明,考查三棱锥体积的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
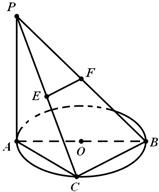 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且PA=AC=BC,E,F分别为PC,PB中点.
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且PA=AC=BC,E,F分别为PC,PB中点.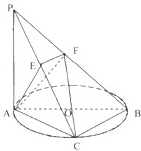 (2013•韶关一模)如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=4,C是⊙O上一点,且PA=AC=BC,
(2013•韶关一模)如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=4,C是⊙O上一点,且PA=AC=BC, 如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点,F为PB中点.
如图,已知PA⊥⊙O所在的平面,AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PC与⊙O所在的平面成45°角,E是PC中点,F为PB中点.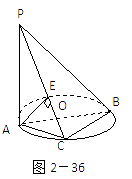 如图:已知PA⊥⊙O所在的平面,AB是⊙O的直径,
如图:已知PA⊥⊙O所在的平面,AB是⊙O的直径,