题目内容
11、已知PA⊥⊙O所在的平面，AB是⊙O的直径，C是⊙O上任意一点，过A点作AE⊥PC于点E，求证：AE⊥平面PBC．分析：根据底面是圆，得到BC⊥AC，再根据PA⊥平面ABC得到PA⊥BC，最后综合即可证明AE⊥平面PBC．
解答：证明：∵PA⊥平面ABC，∴PA⊥BC．
又∵AB是⊙O的直径，∴BC⊥AC．而PC∩AC=C，∴BC⊥平面PAC．
又∵AE在平面PAC内，∴BC⊥AE．
∵PC⊥AE，且PC∩BC=C，
∴AE⊥平面PBC．
又∵AB是⊙O的直径，∴BC⊥AC．而PC∩AC=C，∴BC⊥平面PAC．
又∵AE在平面PAC内，∴BC⊥AE．
∵PC⊥AE，且PC∩BC=C，
∴AE⊥平面PBC．
点评：本题考查直线与平面垂直的判定，通过对已知条件的分析，得到线面垂直，属于基础题．
练习册系列答案
相关题目
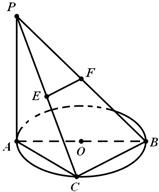如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且PA=AC=BC，E，F分别为PC，PB中点．
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点．F为PB中点．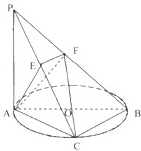
（2013•韶关一模）如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=4，C是⊙O上一点，且PA=AC=BC，
如图，已知PA⊥⊙O所在的平面，AB是⊙O的直径，AB=2，C是⊙O上一点，且AC=BC，PC与⊙O所在的平面成45°角，E是PC中点，F为PB中点．