题目内容
如图,圆柱 内接直三棱柱
内接直三棱柱 ,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且
,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且 。在圆柱
。在圆柱 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱 内的概率为
内的概率为
(1)当点C在圆周上运动时,求 的最大值;
的最大值;
(2)记平面 与平面
与平面 所成的角为
所成的角为
 ,当
,当 取最大值时,求
取最大值时,求 的值。
的值。

解: (1)设圆柱的底面半径为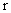 ,则AB=
,则AB=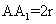 ,故三棱柱
,故三棱柱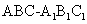 的体积为
的体积为
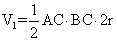 =
=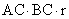 ,又因为
,又因为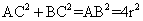 ,
,
所以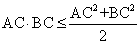 =
=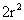 ,当且仅当
,当且仅当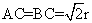 时等号成立,
时等号成立,
从而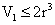 ,而圆柱的体积
,而圆柱的体积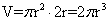 ,
,
故 =
=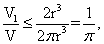 当且仅当
当且仅当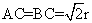 ,即
,即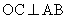 时等号成立,
时等号成立,
所以 的最大值是
的最大值是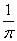 。
。
(2)由(1)可知, 取最大值时,
取最大值时,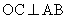 ,于是以O为坐标原点,建立空间直角坐标系
,于是以O为坐标原点,建立空间直角坐标系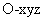 ,则C(r,0,0),B(0,r,0),
,则C(r,0,0),B(0,r,0),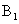 (0,r,2r),
(0,r,2r),
因为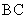
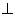 平面
平面 ,所以
,所以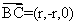 是平面
是平面 的一个法向量,
的一个法向量,
设平面 的法向量
的法向量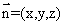 ,由
,由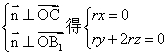 ,故
,故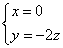 ,
,
取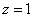 得平面
得平面 的一个法向量为
的一个法向量为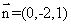 ,因为
,因为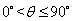 ,
,
所以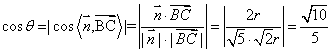 。故
。故 =
=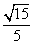

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 ,B
,B ,当
,当 取最小值时,
取最小值时, 的值等于( )
的值等于( ) B.
B.  C.
C.  D.
D. 
 的焦点与双曲线
的焦点与双曲线 的一焦点重合,则该双曲线的
的一焦点重合,则该双曲线的 B.
B. C.
C. D.
D.
 的展开式中常数项等于________.
的展开式中常数项等于________. .
.
 是定义域为
是定义域为 的奇函数,试求实数
的奇函数,试求实数 的值
的值 有三个零点,试求实数
有三个零点,试求实数 的取值范围.
的取值范围. 的取值范围为( )
的取值范围为( ) B.
B. C.
C. D.
D. 
 中,已知
中,已知 ,其前n项和
,其前n项和 满足
满足 .
. 的值;
的值; ;
; ,试求一个函数
,试求一个函数 ,使得对于任意正整数n有
,使得对于任意正整数n有 ,且对于任意的
,且对于任意的 ,均存在
,均存在 ,使得
,使得 时,
时, .
.