题目内容
在数列 中,已知
中,已知 ,其前n项和
,其前n项和 满足
满足
 .
.
(1) 求 的值;
的值;
(2)求数列 的通项公式
的通项公式 ;
;
(3)令 ,试求一个函数
,试求一个函数 ,使得对于任意正整数n有
,使得对于任意正整数n有 ,且对于任意的
,且对于任意的 ,均存在
,均存在 ,使得
,使得 时,
时, .
.
解:(1)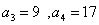 .………………4分
.………………4分
(2)由题设知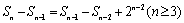 ,即
,即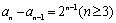 .
.
由累加法可得: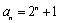 .………………8分
.………………8分
(3)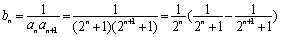 . ………………10分
. ………………10分
则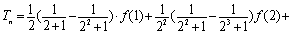 …
…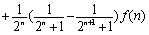 .
.
令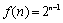 , 则
, 则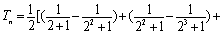 …
…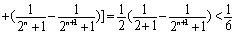 . …12分
. …12分
若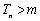 ,则有
,则有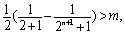 化简得:
化简得: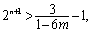 即解不等式
即解不等式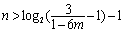 .
.
当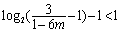 ,即
,即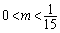 时,取
时,取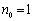 即可. 当
即可. 当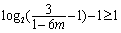 ,即
,即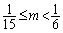 时,则记
时,则记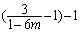 的整数部分为s,取
的整数部分为s,取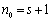 即可. ………………14分
即可. ………………14分
综上可知,对任意 ,均存在
,均存在 ,使得
,使得 时,
时,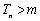 ,即
,即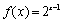 为所求函数.
为所求函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 内接直三棱柱
内接直三棱柱 ,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且
,该三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径,且 。在圆柱
。在圆柱
 与平面
与平面 所成的角为
所成的角为
 ,当
,当 的值。
的值。
 对任意的实数
对任意的实数 ,存在常数
,存在常数 ,使得不等式
,使得不等式 恒成立,那么就称函数
恒成立,那么就称函数 ;②
;② ;③
;③ .其中属于有界泛函的是( )
.其中属于有界泛函的是( ) 的前
的前 项和为
项和为 ,数列
,数列 为等比数列,且
为等比数列,且 .
. ,求数列
,求数列 的前
的前 .
. ,则
,则 的值为( )
的值为( ) B、
B、 C、
C、 D、
D、
 ,且
,且 ,则实数
,则实数
 已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ 的值分别为 ( )
已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ 的值分别为 ( )

 则
则