题目内容
在数列{an}中,已知a1=3,an+1=an+4n-2(n∈N*),则数列{an}的通项为an= .
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:在数列递推式中依次取n=1,2,3,…,(n-1),利用累加法求数列的通项公式.
解答:
解:由an+1=an+4n-2(n∈N*),得
a2-a1=4×1-2,
a3-a2=4×2-2,
a4-a3=4×3-2,
…
an-an-1=4(n-1)-2(n≥2),
累加得:an=a1+4[1+2+3+…+(n-1)]-2(n-1)
=3+4×
-2n+2=2n2-4n+5(n≥2).
验证n=1时上式成立.
∴an=2n2-4n+5.
故答案为:2n2-4n+5.
a2-a1=4×1-2,
a3-a2=4×2-2,
a4-a3=4×3-2,
…
an-an-1=4(n-1)-2(n≥2),
累加得:an=a1+4[1+2+3+…+(n-1)]-2(n-1)
=3+4×
| (n-1)n |
| 2 |
验证n=1时上式成立.
∴an=2n2-4n+5.
故答案为:2n2-4n+5.
点评:本题考查了数列递推式,考查了累加法求数列的通项公式,是中档题.

练习册系列答案
相关题目
已知函数f(x)=ax3+bx2+cx+d(a≠0)的对称中心为M(x0,y0),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x0)=0.若函数f(x)=x3-3x2,则可求出f(
)+f(
)+f(
)+…+f(
)+f(
)的值为( )
| 1 |
| 2015 |
| 2 |
| 2015 |
| 3 |
| 2015 |
| 4028 |
| 2015 |
| 4029 |
| 2015 |
| A、4029 | B、-4029 |
| C、8058 | D、-8058 |
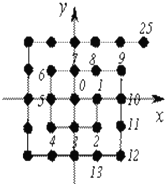 将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )
将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )| A、(1008,1007) |
| B、(1007,1006) |
| C、(1007,1005) |
| D、(1006,1005) |
二进制数1111111111转化为十进制数应该是( )
| A、1023 | B、1024 |
| C、2047 | D、2048 |
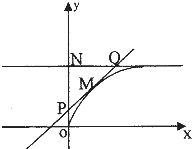 如图为函数f(x)=
如图为函数f(x)=