题目内容
14.设抛物线y2=4x的焦点为F,过F且倾斜角为$\frac{π}{4}$的直线交抛物线于A、B两点,则|AB|=8.分析 根据抛物线解析式确定出焦点F坐标,根据直线AB倾斜角表示出直线AB方程,与抛物线解析式联立消去y得到关于x的一元二次方程,设方程的两根为x1,x2,即A(x1,y1),B(x2,y2),利用根与系数关系及两点间的距离公式求出AB长即可.
解答 解:由题意得:抛物线y2=4x的焦点F为(1,0),
∵直线AB倾斜角为45°,
∴直线AB的斜率为1,即方程为y=x-1,
联立抛物线方程,消去y得:(x-1)2=4x,即x2-6x+1=0,
设方程的两根为x1,x2,即A(x1,y1),B(x2,y2),
则有x1+x2=6,x1x2=1,
则|AB|=$\sqrt{1+1}•\sqrt{36-4}$=8,
故答案为:8.
点评 此题考查了抛物线的简单性质,根与系数关系,两点间的距离公式,以及直线的点斜式方程,熟练掌握抛物线的简单性质是解本题的关键.

练习册系列答案
相关题目
5.有两张卡片,一张的正反面分别画着老鼠和小鸡,另一张的正反面分别画着老鹰和蛇,现在有两个小孩随机地将两张卡片排在一起放在桌面上,不考虑顺序,则向上的图案是老鹰和小鸡的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
9.下列选项中,说法正确的是( )
| A. | 命题“?x0∈R,x02-x0≤0”的否定为“?x∈R,x2-x>0” | |
| B. | 若非零向量$\overrightarrow a$、$\overrightarrow b$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,则$\overrightarrow a$与$\overrightarrow b$共线 | |
| C. | 命题“在△ABC中,A>30°,则sinA>$\frac{1}{2}$”的逆否命题为真命题 | |
| D. | 设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件 |
19.已知集合A={x|x2+5x>0},B={x|-3<x<4},则A∩B等于( )
| A. | (-5,0) | B. | (-3,0) | C. | (0,4) | D. | (-5,4) |
6.已知集合A={x|(x-2)(x+6)>0},B={x|-3<x<4},则A∩B等于( )
| A. | (-3,-2) | B. | (-3,2) | C. | (2,4) | D. | (-2,4) |
3.执行如图所示的程序框图,若输出的结果是6,则判断框内m的取值范围是( )
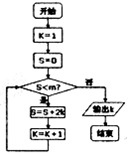

| A. | (30,42] | B. | (20,30) | C. | (20,30] | D. | (20,42) |