题目内容
若二项式(ax+
)6的展开式中含x5的系数为-
,则
x2dx的值为 .
| ||
| 6 |
| 3 |
| ∫ | a -2 |
考点:二项式定理的应用,定积分
专题:计算题,二项式定理
分析:利用二项展开式的第二项系数,求出a的值,根据积分公式计算可得答案.
解答:
解:∵二项式(ax+
)6的展开式中含x5的系数为
•a5•
=
•a5=-
,
∴a=-1,
∴
x2dx=
x3|
=
[(-1)3-(-2)3|=
.
故答案为:
.
| ||
| 6 |
| C | 1 6 |
| ||
| 6 |
| 3 |
| 3 |
∴a=-1,
∴
| ∫ | a -2 |
| 1 |
| 3 |
-1 -2 |
| 1 |
| 3 |
| 7 |
| 3 |
故答案为:
| 7 |
| 3 |
点评:本题考查了二项展开式的通项公式,考查了积分运算,解答的关键是熟记积分公式.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
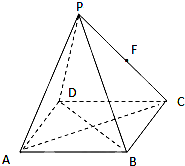 如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PA=PB=PC=PD,F为PC中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PA=PB=PC=PD,F为PC中点.