题目内容
在平面直角坐标系xOy中,设椭圆T的中心在坐标原点,一条准线方程为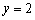 ,且经过点(1,0).
,且经过点(1,0).
(1)求椭圆T的方程;
(2)设四边形ABCD是矩形,且四条边都与椭圆T相切.求证:满足条件的所有矩形的顶点在一个定圆上;
(1)因为椭圆T的中心在坐标原点,一条准线方程为y=2,
所以椭圆T的焦点在y轴上,于是可设椭圆T的方程为 +
+ =1(a>b>0).
=1(a>b>0).
因为椭圆T经过点(1,0),
所以 解得
解得
故椭圆T的方程为 .
.
(2)由题意知,矩形ABCD是椭圆 的外切矩形,
的外切矩形,
(i)若矩形ABCD的边与坐标轴不平行,则可设一组对边所在直线的方程为 ,
,
则由 消去y得
消去y得 ,
,
于是 ,化简得
,化简得 .
.
所以矩形ABCD的一组对边所在直线的方程为 ,即
,即 ,
,
则另一组对边所在直线的方程为 ,
,
于是矩形顶点坐标(x,y)满足 ,
,
即 ,亦即
,亦即 .
.
(ii)若矩形ABCD的边与坐标轴平行,则四个顶点 显然满足
显然满足 .
.
故满足条件的所有矩形的顶点在定圆 上.
上.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 且
且 ,集合
,集合 的所有
的所有 个元素的子集记为
个元素的子集记为 .
. ;
; 为
为
 中最小元素与最大元素之和,求
中最小元素与最大元素之和,求 的值.
的值. .
. ;
; 的取值范围
的取值范围
 的参数方程是
的参数方程是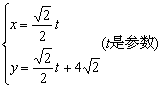 ,圆C的极坐标方程为
,圆C的极坐标方程为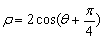 .
.

 如图在
如图在 中,AB=AC,过点A的直线与
中,AB=AC,过点A的直线与
 在
在 上单调递增,则实数
上单调递增,则实数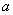 的取值范围是 .
的取值范围是 .