题目内容
3.记Sn为正项等比数列{an}的前n项和,若$\frac{{S}_{12}-{S}_{6}}{{S}_{6}}$-7•$\frac{{S}_{6}-{S}_{3}}{{S}_{3}}$-8=0,且正整数m,n满足a1ama2n=2${a}_{5}^{3}$,则$\frac{1}{m}$+$\frac{8}{n}$的最小值是( )| A. | $\frac{7}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{9}{5}$ | D. | $\frac{15}{7}$ |
分析 根据已知可得正项等比数列{an}的公比为q=2,进而根据等比数列的性质可得m+2n=15,结合基本不等式可得答案.
解答 解:设正项等比数列{an}的公比为q,则q>0,
∵$\frac{{S}_{12}-{S}_{6}}{{S}_{6}}$-7•$\frac{{S}_{6}-{S}_{3}}{{S}_{3}}$-8=0,
∴q6-7q3-8=0,
解得:q=2,或q=-1(舍去),
若正整数m,n满足a1ama2n=2${a}_{5}^{3}$,
则m+2n=15,
则$\frac{1}{m}$+$\frac{8}{n}$=($\frac{1}{m}$+$\frac{8}{n}$)($\frac{m+2n}{15}$)=$\frac{17}{15}$+$\frac{2n}{15m}$+$\frac{8m}{15n}$≥$\frac{17}{15}$+2$\sqrt{\frac{2n}{15m}•\frac{8m}{15n}}$=$\frac{5}{3}$,
当且仅当$\frac{2n}{15m}$=$\frac{8m}{15n}$,即m=3,n=6时,取等号,
故$\frac{1}{m}$+$\frac{8}{n}$的最小值是$\frac{5}{3}$,
故选:B.
点评 本题考查的知识点是等比数列的性质,基本不等式,是不等式与数列的综合应用,难度中档.

练习册系列答案
相关题目
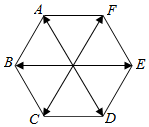 如图,在正六边形ABCDEF中,与$\overrightarrow{OA}$-$\overrightarrow{OC}$+$\overrightarrow{CD}$相等的向量有①.(填序号)
如图,在正六边形ABCDEF中,与$\overrightarrow{OA}$-$\overrightarrow{OC}$+$\overrightarrow{CD}$相等的向量有①.(填序号)