题目内容
已知椭圆的中心在原点,焦点 在
在 轴的非负半轴上,点
轴的非负半轴上,点 到短
到短
轴端点的距离是4,椭圆上的点到焦点 距离的最大值是6.
距离的最大值是6.
(1)求椭圆的标准方程和离心率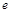 ;
;
(2)若 为焦点
为焦点 关于直线
关于直线 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使 到点
到点 的距离为定值?若存在,求出点
的距离为定值?若存在,求出点 的坐标及此定值;若不存在,请说明理由.
的坐标及此定值;若不存在,请说明理由.
 在
在 轴的非负半轴上,点
轴的非负半轴上,点 到短
到短轴端点的距离是4,椭圆上的点到焦点
 距离的最大值是6.
距离的最大值是6.(1)求椭圆的标准方程和离心率
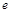 ;
;(2)若
 为焦点
为焦点 关于直线
关于直线 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使 到点
到点 的距离为定值?若存在,求出点
的距离为定值?若存在,求出点 的坐标及此定值;若不存在,请说明理由.
的坐标及此定值;若不存在,请说明理由.(1) 椭圆的标准方程为 . 离心率
. 离心率
(2)存在一个定点 ,使
,使 到
到 点的距离为定值,其定值为
点的距离为定值,其定值为
 . 离心率
. 离心率
(2)存在一个定点
 ,使
,使 到
到 点的距离为定值,其定值为
点的距离为定值,其定值为
本试题主要是考查了椭圆方程的求解以及轨迹方程的求解来判定点是否存在。
(1)根据已知中椭圆的几何性质得关于参数a,b,c的关系式,进而解得。
(2)利用比值为定值,设出点的坐标,然后利用M的轨迹方程求解得到结论。
解:(1)设椭圆长半轴长及半焦距分别为 ,由已知得
,由已知得
 .
.
所以椭圆的标准方程为 .……………………6分
.……………………6分
离心率 …………………………7分
…………………………7分
(2) ,设
,设 由
由 得
得
 ……………………10分
……………………10分
化简得 ,即
,即 ……………………12分
……………………12分
故存在一个定点 ,使
,使 到
到 点的距离为定值,其定值为
点的距离为定值,其定值为 ………13分
………13分
(1)根据已知中椭圆的几何性质得关于参数a,b,c的关系式,进而解得。
(2)利用比值为定值,设出点的坐标,然后利用M的轨迹方程求解得到结论。
解:(1)设椭圆长半轴长及半焦距分别为
 ,由已知得
,由已知得 .
. 所以椭圆的标准方程为
 .……………………6分
.……………………6分离心率
 …………………………7分
…………………………7分(2)
 ,设
,设 由
由 得
得 ……………………10分
……………………10分化简得
 ,即
,即 ……………………12分
……………………12分故存在一个定点
 ,使
,使 到
到 点的距离为定值,其定值为
点的距离为定值,其定值为 ………13分
………13分 
练习册系列答案
相关题目
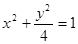 的离心率为( )
的离心率为( )


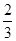
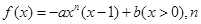 为正整数,
为正整数,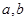 为常数.曲线
为常数.曲线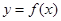 在点
在点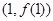 处的切线方程为
处的切线方程为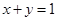 .
.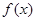 的最大值;
的最大值;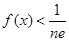 .
. 过双曲线
过双曲线
 右焦点,交双曲线于
右焦点,交双曲线于 ,
, 两点,
两点, 的最小值为2,则其离心率为( )
的最小值为2,则其离心率为( )

 的焦点,离心率是
的焦点,离心率是
 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由. +
+ =1的离心率 e =
=1的离心率 e = , 则k的值是
, 则k的值是  轴上,一个顶点为
轴上,一个顶点为 ,且其右焦点到直线
,且其右焦点到直线 的距离为3.
的距离为3. ,且过定点
,且过定点 的直线
的直线 ,使
,使 、
、 ,且
,且 ?若存在,求出直线
?若存在,求出直线 的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________
的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,则△OAB的面积为______________ 的焦点为
的焦点为 和
和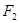 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
轴上,那么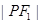 是
是 的( )
的( ) 倍
倍 倍
倍 倍
倍 倍
倍