题目内容
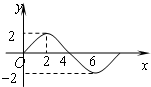函数f（x）的部分图象如图所示，则f（1）+f（2）+…+f（2010）+f（2011）的值为2(
+1)
| 2 |
2(
+1)
．| 2 |
分析：由图象推出函数的周期，求出函数的解析式，求出一个周期内的函数值的和，然后求解表达式的值．
解答：解：由题意以及函数的图象可知，函数的周期为8，A=2，ω=
=
，函数的解析式为y=2sin
x，
f（1）+f（2）+…+f（8）=2sin
+2sin
+2sin
+2sin
+2sin
+2sin+
+sin
+sin
=0；
所以f（1）+f（2）+…+f（2010）+f（2011）=f（1）+f（2）+f（3）+253×[f（1）+f（2）+…+f（8）]
=f（1）+f（2）+f（3）
=2sin
+2sin
+2sin
=
+2+
=2
+2．
故答案为：2（
+1）．
| 2π |
| T |
| π |
| 4 |
| π |
| 4 |
f（1）+f（2）+…+f（8）=2sin
| π |
| 4 |
| 2π |
| 4 |
| 3π |
| 4 |
| 4π |
| 4 |
| 5π |
| 4 |
| 6π |
| 4 |
| 7π |
| 4 |
| 8π |
| 4 |
所以f（1）+f（2）+…+f（2010）+f（2011）=f（1）+f（2）+f（3）+253×[f（1）+f（2）+…+f（8）]
=f（1）+f（2）+f（3）
=2sin
| π |
| 4 |
| 2π |
| 4 |
| 3π |
| 4 |
=
| 2 |
| 2 |
=2
| 2 |
故答案为：2（
| 2 |
点评：本题是中档题，考查三角函数的解析式的求法，三角函数的周期的应用，注意一个周期内的函数的值的求法以及，表达式的剩余项是解题的关键，考查计算能力．
练习册系列答案
相关题目
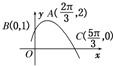已知函数f（x）的部分图象如图所示，则f（x）的解析式可能为（ ）A、f（x）=2cos（
| ||||
B、f（x）=
| ||||
C、f（x）=2sin（
| ||||
D、f（x）=2sin（4x+
|
已知函数f（x）=Asin（ωx+?）（A＞0，ω＞0，0＜?＜π），其导函数f′（x）的部分图象如图所示，则函数f（x）的解析式为
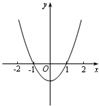5、已知可导函数f（x）的导函数f′（x）的部分图象如图所示，则函数f（x+1）的部分图象可能是（ ）
函数f（x）的部分图象如图所示，则f（x）的解析式可能是（ ）
（2011•南通模拟）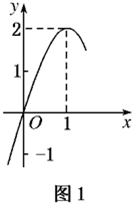
如图所示：图1是定义在R上的二次函数f（x）的部分图象，图2是函数g（x）=loga（x+b）的部分图象．