题目内容
函数f（x）=3ax+1-2a在（-1，1）存在一个零点x0，则a的取值范围是（ ）
A、（-1，
| ||
B、（
| ||
C、（-∞，-1）∪（
| ||
| D、（-∞，-1） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：利用根的存在定理，可得f（-1）f（1）＜0，求解即可．
解答：
解：当a=0时，f（x）=1，此时函数在（-1，1）上不存在零点，所以a≠0．
要使f（x）=3ax+1-2a在（-1，1）上存在零点，则有f（-1）f（1）＜0，
即（3a+1-2a）（-3a+1-2a）＜0，所以（a+1）（5a-1）＞0，
解得a＞
或a＜-1．
故选：C．
要使f（x）=3ax+1-2a在（-1，1）上存在零点，则有f（-1）f（1）＜0，
即（3a+1-2a）（-3a+1-2a）＜0，所以（a+1）（5a-1）＞0，
解得a＞
| 1 |
| 5 |
故选：C．
点评：本题主要考查函数零点的应用．基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
（3-4i）（1-2i）2等于（ ）
| A、-9 | B、-25 |
| C、-9i | D、-25i |
已知m、n是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是（ ）
| A、若m∥n，m∥α，则n∥α |
| B、若m⊥α，n⊥α，则m∥n |
| C、若n⊥α，m⊥β，则m⊥n |
| D、若α∥β，n⊥β，则m⊥α |
给出下列函数：
①f（x）=（
）x；
②f（x）=x2；
③f（x）=x3；
④f（x）=x
；
⑤f（x）=log2x．
其中满足条件f（
）＞
（0＜x1＜x2）的函数的个数是（ ）
①f（x）=（
| 1 |
| 2 |
②f（x）=x2；
③f（x）=x3；
④f（x）=x
| 1 |
| 2 |
⑤f（x）=log2x．
其中满足条件f（
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
等差数列{an}中，a3+a13=-8，数列{bn}是等比数列，若b7=a8，则b6•b8的值为（ ）
| A、2 | B、4 | C、8 | D、16 |
已知双曲线
-
=1的右焦点为（3，0），则a的值等于（ ）
| x2 |
| a2 |
| y2 |
| 5 |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
函数y=x2+x
是（ ）
| 1 |
| 2 |
| A、偶函数 | B、奇函数 |
| C、既奇既偶 | D、非奇非偶 |
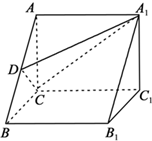如图，在三棱柱ABC-A1B1C1中，AC⊥BC，AB⊥BB1，AC=BC=BB1=2，D为AB的中点，且CD⊥DA1．
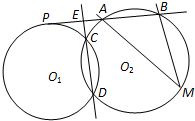已知⊙O1和⊙O2交于点C和D，⊙O1上的点P处的切线交⊙O2于A、B点，交直线CD于点E，M是⊙O2上的一点，若PE=2，EA=1，∠AMB=45°，那么⊙O2的半径为