题目内容
已知集合M={x|sinx=0}，N={x|-1＜x＜4}，则M∩N等于（ ）
| A、{0，π} | ||||
| B、{x|0≤x≤π} | ||||
C、{x|-
| ||||
D、{-
|
考点：交集及其运算
专题：集合
分析：由正弦函数的性质及特殊角的三角函数值求出M中x的值确定出M，找出M与N的交集即可．
解答：
解：由sinx=0，得到x=kπ，k∈Z，即M={x|x=kπ，k∈Z}，
∵N={x|-1＜x＜4}，
∴M∩N={0，π}，
故选：A．
∵N={x|-1＜x＜4}，
∴M∩N={0，π}，
故选：A．
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，A，B，C所对的边长分别是a，b，c且A=30°，B=45°，a=3，则b=（ ）
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
已知f（x）=x2（1nx-a）+a，则下列结论中错误的是（ ）
| A、?a＞0，?x＞0，f（x）≥0 |
| B、?a＞0，?x＞0，f（x）≤0 |
| C、?a＞0，?x＞0，f（x）≥0 |
| D、?a＞0，?x＞0，f（x）≤0 |
已知集合A={1，3，4}，B={1，4，6}，那么A∪B=（ ）
| A、{2，5} |
| B、{1，3，4，6} |
| C、{1，4} |
| D、{2，3，5} |
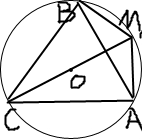如图，在△ABC中，a，b，c分别为∠A，∠B，∠C的对边，a2+b2-c2=ab，CM是△ABC外接圆的直径，BM=11，AM=2，求CM的长．
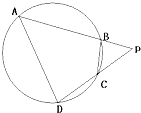如图，四边形ABCD是圆O的内接四边形，延长AB和DC相交于点P．若PB=1，PD=3，则
某篮球队甲、乙两名队员，在预赛中每场比赛得分的原始记录如右茎叶图所示，若要从甲、乙两人中选拔一人参加决赛，则应该选择