题目内容
2.已知直线l:(m+1)x+(2m-1)y+m-2=0,则直线恒过定点(1,-1).分析 直线l:(m+1)x+(2m-1)y+m-2=0,化为:m(x+2y+1)+(x-y-2)=0,联立$\left\{\begin{array}{l}{x+2y+1=0}\\{x-y-2=0}\end{array}\right.$,解出即可得出.
解答 解:直线l:(m+1)x+(2m-1)y+m-2=0,化为:m(x+2y+1)+(x-y-2)=0,
联立$\left\{\begin{array}{l}{x+2y+1=0}\\{x-y-2=0}\end{array}\right.$,解得x=1,y=-1.
则直线恒过定点(1,-1).
故答案为:(1,-1).
点评 本题考查了直线系、直线的交点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.已知两点A(a,3),B(1,-2),若直线AB的倾斜角为135°,则a的值为( )
| A. | 6 | B. | -6 | C. | 4 | D. | -4 |
17.已知一个几何体的三视图如图所示,则该几何体的体积是( )
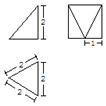

| A. | $2\sqrt{3}$ | B. | $\frac{2}{3}\sqrt{3}$ | C. | $\frac{4}{3}\sqrt{3}$ | D. | $4\sqrt{3}$ |
11.过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则弦AB的长为( )
| A. | 10 | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | $\frac{13}{2}$ |
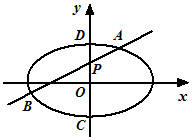 如图,椭圆E:$\frac{x^2}{4}+\frac{y^2}{b^2}=1(0<b<2)$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}•\overrightarrow{PD}=-2$
如图,椭圆E:$\frac{x^2}{4}+\frac{y^2}{b^2}=1(0<b<2)$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}•\overrightarrow{PD}=-2$