题目内容
设a,b>0,a≠b,lna-lnb=a-b,给出下列结论:
①0<ab<1;②0<a+b<2;③a+b-ab>1.
其中所有正确结论的序号是( )
①0<ab<1;②0<a+b<2;③a+b-ab>1.
其中所有正确结论的序号是( )
| A、①② | B、①③ | C、②③ | D、①②③ |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:lna-lnb=a-b,化为lna-a=lnb-b.令f(x)=lnx-x,(x>0),利用导数可得函数f(x)的单调性,画出图象.不妨设0<a<b.0<a<1<b.0<
<1.
①证明ab<1,只要证明f(a)<f(
)即可,即证明lnb-b<ln
-
,化为g(b)=2lnb-b+
<0,(b>1).利用导数研究其单调性即可得出.
②由图象可得b-1>1-a,可得a+b>2,即可判断出正误;
③由图象可得:(a-1)(b-1)<0,化简即可判断出正误.
| 1 |
| b |
①证明ab<1,只要证明f(a)<f(
| 1 |
| b |
| 1 |
| b |
| 1 |
| b |
| 1 |
| b |
②由图象可得b-1>1-a,可得a+b>2,即可判断出正误;
③由图象可得:(a-1)(b-1)<0,化简即可判断出正误.
解答:
解:lna-lnb=a-b,化为lna-a=lnb-b.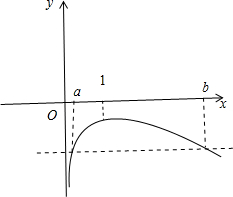
令f(x)=lnx-x,(x>0),
f′(x)=
-1=
,
当x>1时,f′(x)<0,此时函数f(x)单调递减;当0<x<1时,f′(x)>0,此时函数f(x)单调递增.
∴当x=1时,函数f(x)取得最大值,f(1)=-1.
∵a,b>0,a≠b,不妨设0<a<b.
又f(a)=f(b),
则0<a<1<b.0<
<1.
①证明ab<1,只要证明a<
,
∵0<a<
<1,
∴只要证明f(a)<f(
)即可,
∵f(a)=f(b),
∴只要证明f(b)<f(
)即可,
即证明lnb-b<ln
-
,
化为g(b)=2lnb-b+
<0,(b>1).
g′(b)=
-1-
=
<0,
∴函数g(b)在b>1时单调递减,
∴g(b)<g(1)=0,
因此f(b)<f(
)成立,即f(a)<f(
)成立,
∴a<
<1,
∴0<ab<1正确,①正确.
②由图象可得b-1>1-a,∴a+b>2,∴②不正确;
③∵(a-1)(b-1)<0,∴a+b-ab>1,因此③正确.
综上可得:①③正确.
故选:B.

令f(x)=lnx-x,(x>0),
f′(x)=
| 1 |
| x |
| 1-x |
| x |
当x>1时,f′(x)<0,此时函数f(x)单调递减;当0<x<1时,f′(x)>0,此时函数f(x)单调递增.
∴当x=1时,函数f(x)取得最大值,f(1)=-1.
∵a,b>0,a≠b,不妨设0<a<b.
又f(a)=f(b),
则0<a<1<b.0<
| 1 |
| b |
①证明ab<1,只要证明a<
| 1 |
| b |
∵0<a<
| 1 |
| b |
∴只要证明f(a)<f(
| 1 |
| b |
∵f(a)=f(b),
∴只要证明f(b)<f(
| 1 |
| b |
即证明lnb-b<ln
| 1 |
| b |
| 1 |
| b |
化为g(b)=2lnb-b+
| 1 |
| b |
g′(b)=
| 2 |
| b |
| 1 |
| b2 |
| -(b-1)2 |
| b2 |
∴函数g(b)在b>1时单调递减,
∴g(b)<g(1)=0,
因此f(b)<f(
| 1 |
| b |
| 1 |
| b |
∴a<
| 1 |
| b |
∴0<ab<1正确,①正确.
②由图象可得b-1>1-a,∴a+b>2,∴②不正确;
③∵(a-1)(b-1)<0,∴a+b-ab>1,因此③正确.
综上可得:①③正确.
故选:B.
点评:本题考查了利用导数研究函数的单调性极值与最值、证明不等式,考查了数形结合的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=
则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)的值域为[-1+∞) |
| C、f(x)是周期函数 |
| D、f(x)是增函数 |
已知x,y满足
,则
的最小值为( )
|
| (x-2)2+(y+1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若不论k为何值,直线y=k(x-2)+b与曲线x2-y2=1总有公共点,则b的取值范围是( )
A、(-
| ||||
B、[-
| ||||
| C、(-2,2) | ||||
| D、[-2,2] |
已知f(x)=4|x|+x2+a有唯一的零点,则实数a的值为( )
| A、0 | B、-1 | C、-2 | D、-3 |
 已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD,试问:当
已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD,试问:当