题目内容
已知椭圆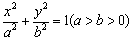 的右焦点为
的右焦点为 ,离心率为e.
,离心率为e.
(1)若 ,求椭圆的方程;
,求椭圆的方程;
(2)设A,B为椭圆上关于原点对称的两点,AF的中点为M,BF的中点为N,若原点O在以线段MN为直径的圆上.
①证明点A在定圆上;②设直线AB的斜率为k,若 ,求e的取值范围.
,求e的取值范围.
[解析](1)由 ,c=2,得a=
,c=2,得a= ,b=2.所求椭圆方程为
,b=2.所求椭圆方程为 .
.
(2)设 ,则
,则 ,故
,故 ,
, .
.
① 由题意,得 .
.
化简,得 ,所以点
,所以点 在以原点为圆心,2为半径的圆上.
在以原点为圆心,2为半径的圆上.
② 设 ,则
,则



 .
.
将 ,
, ,代入上式整理,得
,代入上式整理,得
因为 ,k2>0,所以
,k2>0,所以  ,
, .
.
所以  .化简,得
.化简,得
解之,得 ,
, ,故离心率的取值范围是
,故离心率的取值范围是 .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 与复数
与复数 对应,动点
对应,动点 与复数
与复数 对应,那么满足不等式
对应,那么满足不等式 的点
的点 中,侧棱垂直底面,
中,侧棱垂直底面, ,
, ,
,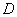 是棱
是棱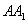 的中点
的中点 平面
平面 ;
; 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
 中,圆C的方程为
中,圆C的方程为 .若直线
.若直线 上存在点
上存在点 ,使过
,使过 的取值范围是 .
的取值范围是 . 分别为
分别为 和椭圆
和椭圆
 上的点,则
上的点,则 中
中 ,前
,前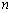 项和为
项和为 ,
,
 ,则
,则 的值为___ __.
的值为___ __.
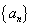 中,若
中,若 ,
, ,则
,则 的值是 .
的值是 .
 有3个不同的零点,则实数a的取值范围是 .
有3个不同的零点,则实数a的取值范围是 .