题目内容
4. 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2,点E位PC的中点
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥DC,∠ADC=90°,AB=AD=PD=1,CD=2,点E位PC的中点(Ⅰ)求证:BC⊥平面PBD;
(Ⅱ)求E到平面PBD的距离.
分析 (Ⅰ)由已知推导出PD⊥底面ABCD,BC⊥BD,由此能证明BC⊥平面PBD.
(Ⅱ)由 BC⊥平面PBD,能求出E到平面PBD的距离.
解答 证明:(Ⅰ)∵侧面PCD⊥底面ABCD于CD,PD?面PCD,PD⊥CD,
∴PD⊥底面ABCD,
∵BC?面ABCD,∴PD⊥BC
在Rt△ABD中,AB=AD=1,故$BD=\sqrt{2}$,
在直角梯形ABCD中,AB=AD=1,CD=2,故$BC=\sqrt{2}$
由BC2+BD2=CD2,得BC⊥BD,
又∵PD⊥BC,PD∩DB=D,
∴BC⊥平面PBD.…(6分)
解:(Ⅱ)由(Ⅰ)知 BC⊥平面PBD,
E为平面PBD的斜线段PC的中点,
故E到平面PBD的距离$d=\frac{1}{2}|BC|=\frac{{\sqrt{2}}}{2}$.
点评 本题考查线面垂直的证明,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 △ABC中,AB=5,AC=12,BC=13,P为△ABC平面外一点,PA=PB=PC=7
△ABC中,AB=5,AC=12,BC=13,P为△ABC平面外一点,PA=PB=PC=7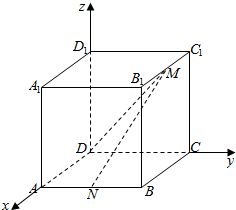 在长方体ABCD-A1B1C1D1中,|AB|=|BC|=2,|D1D|=3,点M是B1C1的中点,点N是AB的中点.建立如图所示的空间直角坐标系.
在长方体ABCD-A1B1C1D1中,|AB|=|BC|=2,|D1D|=3,点M是B1C1的中点,点N是AB的中点.建立如图所示的空间直角坐标系.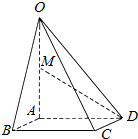 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
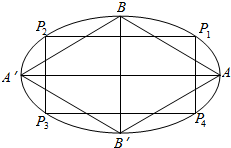 如图,在椭圆中,A′A,B′B分别是长轴,短轴,P1P2P3P4是各边皆平行于对称轴的内接矩形,四边形A′B′AB,P1P2P3P4的面积分别记作Q,S.求证:S≤Q.
如图,在椭圆中,A′A,B′B分别是长轴,短轴,P1P2P3P4是各边皆平行于对称轴的内接矩形,四边形A′B′AB,P1P2P3P4的面积分别记作Q,S.求证:S≤Q.