题目内容
已知，b＞a＞0，x＞y＞0．求证：
＞
．
| x |
| a+x |
| y |
| b+y |
分析：法一：利用作差法，通分后再利用题设中所给条件即可证得
＞
．
法二：利用分析法进行证明．要证
＞
，只需证明x（y+b）＞y（x+a），即证xb＞ya．
| x |
| a+x |
| y |
| b+y |
法二：利用分析法进行证明．要证
| x |
| a+x |
| y |
| b+y |
解答：证法一：（作差比较法）
∵b＞a＞0，x＞y＞0，
∴bx＞ay．
∴
-
=
＞0，
∴
＞
．
证法二：（分析法）
∵b＞a＞0，x＞y＞0，
∴要证
＞
，
只需证明x（y+b）＞y（x+a），即证xb＞ya．
而由b＞a＞0，x＞y＞0，知xb＞ya成立．
故原不等式成立．
故
＞
．
∵b＞a＞0，x＞y＞0，
∴bx＞ay．
∴
| x |
| a+x |
| y |
| b+y |
| bx-ay |
| (x+a)(y+b) |
∴
| x |
| a+x |
| y |
| b+y |
证法二：（分析法）
∵b＞a＞0，x＞y＞0，
∴要证
| x |
| a+x |
| y |
| b+y |
只需证明x（y+b）＞y（x+a），即证xb＞ya．
而由b＞a＞0，x＞y＞0，知xb＞ya成立．
故原不等式成立．
故
| x |
| a+x |
| y |
| b+y |
点评：本题主要考查不等式的证明，比较法是证明不等式的一种最重要最基本的方法．本题还可以利用分析法进行证明．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
(a >0)与x轴的正半轴交于点P．点Q的坐
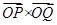=6．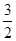
的直线交椭圆C于A、B两点，求△AOB的面积
．
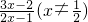）+F（
）+…+F（
）；
}为等差数列（n∈N*），并求数列{an}的通项公式；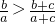
，利用此结论，求证：a1a2…an＞
（n∈N*）．
．