题目内容
已知函数F(x)=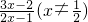 .
.
(I)求F( )+F(
)+F( )+…+F(
)+…+F( );
);
(II)已知数列{an}满足a1=2,an+1=F(an),证明{ }为等差数列(n∈N*),并求数列{an}的通项公式;
}为等差数列(n∈N*),并求数列{an}的通项公式;
(III)已知若b>a>0,c>0,则必有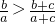 ,利用此结论,求证:a1a2…an>
,利用此结论,求证:a1a2…an> (n∈N*).
(n∈N*).
解:(I)∵F(x)=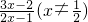 ,
,
∴F(x)+F(1-x)=
=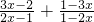 =
=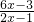 =3,
=3,
设S=F( )+F(
)+F( )+…+F(
)+…+F( ),①
),①
则S=F( )+F(
)+F( )+…+F(
)+…+F( ),②
),②
①+②,得2S=[F( )+F(
)+F( )]+[F(
)]+[F( )+F(
)+F( )]+…+[F(
)]+…+[F( )+F(
)+F( )]=3×2010=6030,
)]=3×2010=6030,
∴S=3015,
∴F( )+F(
)+F( )+…+F(
)+…+F( )=3015.
)=3015.
(II)将等式an+1=F(an)的两边同时减去1,
得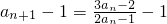 =
=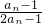 ,
,
∴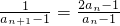 =
=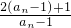 =2+
=2+ ,
,
即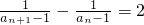 ,又
,又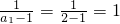 ,
,
∴数列{ }是以2为公差,1为首项的等差数列,
}是以2为公差,1为首项的等差数列,
所以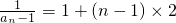 =2n-1,
=2n-1,
所以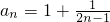 =
=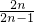 .
.
(III)∵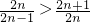 ,
,
∴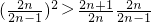 =
=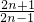 ,
,
∴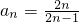 >
>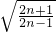 ,
,
∴a1a2…an>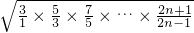 =
= (n∈N*).
(n∈N*).
分析:(I)由F(x)=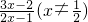 ,得F(x)+F(1-x)=3,设S=F(
,得F(x)+F(1-x)=3,设S=F( )+F(
)+F( )+…+F(
)+…+F( ),利用倒序相加法能求出F(
),利用倒序相加法能求出F( )+F(
)+F( )+…+F(
)+…+F( )的值.
)的值.
(II)将等式an+1=F(an)的两边同时减去1,得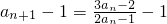 =
=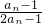 ,由此能证明证明{
,由此能证明证明{ }为等差数列(n∈N*),并求数列{an}的通项公式.
}为等差数列(n∈N*),并求数列{an}的通项公式.
(III)由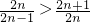 ,得
,得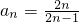 >
>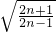 ,由此能够证明a1a2…an>
,由此能够证明a1a2…an> (n∈N*).
(n∈N*).
点评:本题考查数列的通项公式的求法,考查等差数列的证明,解题时要认真审题,仔细解答,注意构造法和放缩法的合理运用.
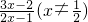 ,
,∴F(x)+F(1-x)=

=
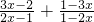 =
=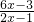 =3,
=3,设S=F(
 )+F(
)+F( )+…+F(
)+…+F( ),①
),①则S=F(
 )+F(
)+F( )+…+F(
)+…+F( ),②
),②①+②,得2S=[F(
 )+F(
)+F( )]+[F(
)]+[F( )+F(
)+F( )]+…+[F(
)]+…+[F( )+F(
)+F( )]=3×2010=6030,
)]=3×2010=6030,∴S=3015,
∴F(
 )+F(
)+F( )+…+F(
)+…+F( )=3015.
)=3015.(II)将等式an+1=F(an)的两边同时减去1,
得
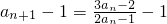 =
=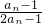 ,
,∴
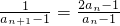 =
=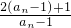 =2+
=2+ ,
,即
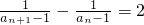 ,又
,又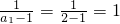 ,
,∴数列{
 }是以2为公差,1为首项的等差数列,
}是以2为公差,1为首项的等差数列,所以
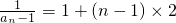 =2n-1,
=2n-1,所以
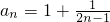 =
=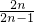 .
.(III)∵
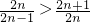 ,
,∴
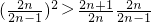 =
=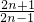 ,
,∴
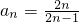 >
>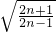 ,
,∴a1a2…an>
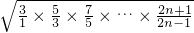 =
= (n∈N*).
(n∈N*).分析:(I)由F(x)=
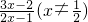 ,得F(x)+F(1-x)=3,设S=F(
,得F(x)+F(1-x)=3,设S=F( )+F(
)+F( )+…+F(
)+…+F( ),利用倒序相加法能求出F(
),利用倒序相加法能求出F( )+F(
)+F( )+…+F(
)+…+F( )的值.
)的值.(II)将等式an+1=F(an)的两边同时减去1,得
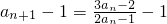 =
=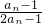 ,由此能证明证明{
,由此能证明证明{ }为等差数列(n∈N*),并求数列{an}的通项公式.
}为等差数列(n∈N*),并求数列{an}的通项公式.(III)由
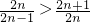 ,得
,得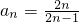 >
>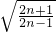 ,由此能够证明a1a2…an>
,由此能够证明a1a2…an> (n∈N*).
(n∈N*).点评:本题考查数列的通项公式的求法,考查等差数列的证明,解题时要认真审题,仔细解答,注意构造法和放缩法的合理运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|