题目内容
已知数列{an}满足:a1=1,an=an-1+n,(n≥2,n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=
| 1 |
| an |
考点:数列的求和,数列递推式
专题:计算题,点列、递归数列与数学归纳法
分析:(Ⅰ)由已知,得an-an-1=n(n≥2,n∈N*),利用累加法求通项公式
(Ⅱ)bn=
=
=2(
-
),利用裂项求和法求数列{bn}的前n项和Sn
(Ⅱ)bn=
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(Ⅰ)an-an-1=n(n≥2,n∈N*)
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+2+3+…+n=
,(n∈N*)
当n=1时满足上式,∴an=
.
(Ⅱ)bn=
=
=2(
-
)
∴Sn=b1+b2+…+bn
=2[(1-
)+(
-
)+…+(
-
)]
=
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=1+2+3+…+n=
| n(n+1) |
| 2 |
当n=1时满足上式,∴an=
| n(n+1) |
| 2 |
(Ⅱ)bn=
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=b1+b2+…+bn
=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 2n |
| n+1 |
点评:本题考查累加法,裂项法在数列计算中的应用,考查计算能力.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
设a>0且a≠1.若logax>sin2x对x∈(0,
)恒成立,则a的取值范围是( )
| π |
| 4 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、[
|
若U={1,2,3,4,5,6,7,8},A={1,3,4},B={5,6,7},则(∁UA)∩(∁UB)=( )
| A、{2,8} |
| B、{2,6,8} |
| C、{1,3,5,7} |
| D、{1,2,3,5,6,7} |
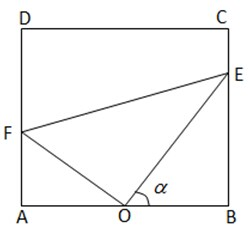 南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25
南海中学校园内建有一块矩形草坪ABCD,AB=50米,BC=25