题目内容

将点的直角坐标（
π
2
，
-
3
π
2
）化为极坐标（ρ＞0，θ∈[0，2π））为
 
．
考点：点的极坐标和直角坐标的互化
专题：坐标系和参数方程
分析：利用ρ=
x2+y2
，tanθ=
y
x
，及点所在的象限即可得出．
解答： 解：ρ=
(
π
2
)2+(-
3
π
2
)2
=π．
tanθ=
-
3
π
2
π
2
=-
3
，
∵点的直角坐标为（
π
2
，
-
3
π
2
）在第四象限，
∴θ=
5π
3
．
∴此点的极坐标为(π，
5π
3
)．
故答案为：(π，
5π
3
)．
点评：本题考查了直角坐标化为极坐标的方法，属于基础题．
练习册系列答案
相关题目
已知x、y、z是互不相等的正实数，且x+y+z=1．求证：（
1
x
-1）（
1
y
-1）（
1
z
-1）＞8．
已知数列{an}，{bn}满足：bn=an+1-λan（n∈N*）．
（1）若λ=1，a1=1，bn=2n，求数列{an}的通项公式；
（2）若λ=-1，a1=a，a2=3a，bn=4n-1，且{an}是递增数列，求a的取值范围；
（3）若λ=1，bn+1bn-1=bn（n≥2），且b1=1，b2=2，记cn=a6n-1（n∈N*），求证：数列{cn}为等差数列．
设数列{an}的前n项和为Sn，点（an，Sn）在直线x+y-2=0上，n∈N*．
（1）证明数列{an}为等比数列，并求出其通项；
（2）设f（n）=log 
1
2
an，记bn=an+1•f（n+1），求数列{bn}的前n项和Tn．
y=sin（x-
π
12
）•cos（x-
π
12
），正确的是（　　）
A、T=2π，对称中心为（
π
12
，0）
B、T=π，对称中心为（
π
12
，0）
C、T=2π，对称中心为（
π
6
，0）
D、T=π，对称中心为（
π
6
，0）
已知命题p：若x2+y2=0，则x、y全为0；命题q：若a＞b，则
1
a
＜
1
b
．给出下列四个复合命题：①p且q，
②p或q，③?p④?q，其中是命题的是
 
．
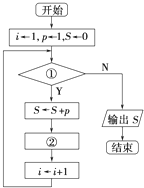给出30个数：1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，依此类推．要计算这30个数的和，现已给出了该问题算法的流程图如图所示．请根据流程图，将下列伪代码补充完整．
若m＞0，0＜n＜1，则函数y=m+lognx的图象可能是（　　）
A、
B、
C、
D、
定义在R上的奇函数f（x）满足：f（2）=0，f（x）=f（x+3），求f（x）=0在x∈[0，3]上的解
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网