题目内容
1.已知函数f(x)是R上的偶函数,若对于x≥0,都有f(x+2)=f(x),且当x∈[0,2)时,f(x)=log2(x+1),则f(-2014)+f(2015)的值为( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 由函数的性质可得f(-2014)+f(2015)=f(0)+f(1)=log2(1+0)+log2(1+1),计算对数可得.
解答 解:∵函数f(x)是R上的偶函数,
∴f(-2014)=f(2014),
又∵对于x≥0,都有f(x+2)=f(x),
∴f(-2014)+f(2015)=f(2014)+f(2015)
=f(0)+f(1)=log2(1+0)+log2(1+1)=0+1=1
故选:C
点评 本题考查函数的周期性和奇偶性,涉及对数函数的运算,属基础题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
13.已知点A(1,1),点P在曲线f(x)=x3-3x2+3x(0≤x≤2)上,点Q在直线y=3x-14上,M为线段PQ的中点,则|AM|的最小值为( )
| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\sqrt{10}$ | D. | $\frac{7\sqrt{10}}{5}$ |
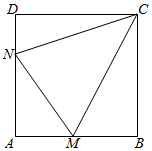 如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上.
如图所示,某村积极开展“美丽乡村•生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. 为检验寒假学生自主学生的效果,级部对某班50名学生各科的检测成绩进行了统计,下面是物理成绩的频率分布直方图,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].
为检验寒假学生自主学生的效果,级部对某班50名学生各科的检测成绩进行了统计,下面是物理成绩的频率分布直方图,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].