题目内容

已知点F1、F2分别为双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点，P为双曲线左支上的任意一点，若|PF2|=2|PF1|，且△PF1F2的周长为9a，则双曲线的离心率为
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用双曲线的定义，结合|PF2|=2|PF1|，可得|PF2|=4a，|PF1|=a，根据△PF1F2的周长为9a，即可求出双曲线的离心率．
解答： 解：∵|PF2|=2|PF1|，|PF2|-|PF1|=2a，
∴|PF2|=4a，|PF1|=a，
∵△PF1F2的周长为9a，
∴2a+4a+2c=9a，
∴
c
a
=
3
2
．
故答案为：
3
2
．
点评：本题考查双曲线的定义与离心率，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知函数f（x）=3x+lnx+
4
x
+1（自然对数的底数e=2.71828…）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）求函数f（x）在[
1
e
，e]上的最大值与最小值．
已知函数f（x）=|x-m|，
（Ⅰ）求证：f（-x）+f（
1
x
）≥2；
（Ⅱ）若m=1且a+b+c=
2
7
时，f（log2x）+f（2+log2x）＞
a
+2
b
+3
c
对任意正数a，b，c恒成立，求实数x的取值范围．
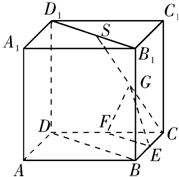如图所示，在正方体ABCD-A1B1C1D1中，S是B1D1的中点，E、F、G分别是BC、CD和SC的中点．求证：
（1）直线EG∥平面BDD1B1；
（2）平面EFG∥平面BDD1B1．
已知A={x|x2-3x+2=0}，B={x|x2-ax+2=0}，若A∪B=A，则a的取值集合为
 
．
已知集合A={x|x2-x-2＞0}，B={x||x-a|≤1}，若A∩B=∅，则实数a的取值范围是
 
．
向量
a
=（k，-2），
b
=（2，2），
a
+
b
为非零向量，若
a
⊥（
a
+
b
），则k=
 
．
极坐标系中，曲线C1：
x=t+2
y=1-2t
（t为参数）和曲线C2：
x=3cosθ
y=3sinθ
相交于点A，B，则线段AB的长度为
 
．
用列举法表示集合：M={m∈Z|
10
m
∈Z}=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网