题目内容
tan240°=
A. | B. | C.1 | D. |
D
解析试题分析:tan240°=tan(180°+60°)=tan60°= ,故选D。
,故选D。
考点:本题主要考查三角函数诱导公式,特殊角的三角函数值。
点评:简单题,应用公式计算。

练习册系列答案
相关题目
函数 的相邻两条对称轴之间的距离为 ( )
的相邻两条对称轴之间的距离为 ( )
A. | B. | C. | D. |
要得到函数y=cos(2x+1)的图象,只需将函数y=cos2x的图象
| A.向左平移1个单位 | B.向右平移1个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
已知奇函数f(x)在[-1,0]上为单调递减函数,又a,b为锐角三角形两内角,下列结论正确的是
| A.f(cosa)> f(cosb) | B.f(sina)> f(sinb) |
| C.f(sina)> f(cosb) | D.f(sina)<f(cosb) |
化简 等于
等于
A. | B. | C. | D. |
已知函数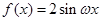 在区间
在区间 上的最小值是
上的最小值是 ,则
,则 的取值范围为( )
的取值范围为( )
A. | B. |
C. | D. |
设函数 与函数
与函数 的对称轴完全相同,则
的对称轴完全相同,则 的值为( )
的值为( )
A. | B. | C. | D. |
若角 的终边上有一点
的终边上有一点 ,则
,则 的值是( )
的值是( )
A. | B. | C. | D. |
函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将
的图象,则只需将 的图象( )
的图象( )
A.向右平移 个长度单位 个长度单位 | B.向右平移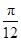 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向左平移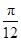 个长度单位 个长度单位 |