题目内容
已知奇函数f(x)在[-1,0]上为单调递减函数,又a,b为锐角三角形两内角,下列结论正确的是
| A.f(cosa)> f(cosb) | B.f(sina)> f(sinb) |
| C.f(sina)> f(cosb) | D.f(sina)<f(cosb) |
D
解析试题分析:∵奇函数y=f(x)在[-1,0]上为单调递减函数,∴f(x)在[0,1]上为单调递减函数,∴f(x)在[-1,1]上为单调递减函数。
又α、β为锐角三角形的两内角
∴α+β> ,∴α>
,∴α> -β
-β
∴sinα>sin( -β)=cosβ>0
-β)=cosβ>0
∴f(sinα)<f(cosβ)
故选D。
考点:本题主要考查函数的奇偶性、单调性,三角函数诱导公式。
点评:小综合题,利用奇函数的性质确定f(x)在[-1,1]上为单调递减函数。利用诱导公式得到sinα>sin( -β)=cosβ>0 。
-β)=cosβ>0 。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知扇形的圆心角为2,半径为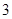 ,则扇形的面积是( )
,则扇形的面积是( )
| A.18 | B.6 | C.3 | D.9 |
函数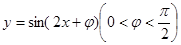 图象的一条对称轴在
图象的一条对称轴在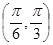 内,则满足此条件的一个
内,则满足此条件的一个 值为
值为
A.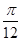 | B.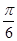 | C.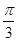 | D.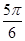 |
设函数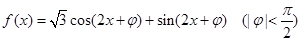 ,且其图象关于直线
,且其图象关于直线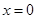 对称,则 ( )
对称,则 ( )
A.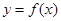 的最小正周期为 的最小正周期为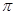 ,且在 ,且在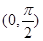 上为增函数 上为增函数 |
B.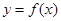 的最小正周期为 的最小正周期为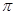 ,且在 ,且在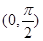 上为减函数 上为减函数 |
C.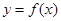 的最小正周期为 的最小正周期为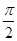 ,且在 ,且在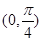 上为增函数 上为增函数 |
D.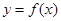 的最小正周期为 的最小正周期为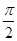 ,且在 ,且在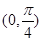 上为减函数 上为减函数 |
 的值等于
的值等于
A. | B. | C. | D. |
tan240°=
A. | B. | C.1 | D. |
为了得到函数 的图像,只需把函数
的图像,只需把函数 的图像( )
的图像( )
A.向左平移 个长度单位 个长度单位 | B.向右平移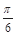 个长度单位 个长度单位 |
C.向左平移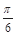 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
已知 =
= ,0<x<π,则tanx为( )
,0<x<π,则tanx为( )
A.- | B.- | C.2 | D.-2 |
若关于x的不等式 在闭区间
在闭区间 上恒成立,则实数
上恒成立,则实数 的取值范围是:( )
的取值范围是:( )
A. | B. | C. | D. |