题目内容
函数 的相邻两条对称轴之间的距离为 ( )
的相邻两条对称轴之间的距离为 ( )
A. | B. | C. | D. |
A
解析试题分析:∵函数 的周期
的周期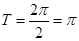 ,∴函数
,∴函数 的相邻两条对称轴之间的距离为
的相邻两条对称轴之间的距离为 ,故选A
,故选A
考点:本题考查了三角函数的周期性
点评:解决此类问题的关键是正确理解题意,通过数形结合,准确找出隐含的最小正周期的个数,将问题化归为我们熟悉的正弦函数、余弦函数及正切函数的最小正周期问题加以解决

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
 等于( )
等于( )
A. | B. | C. | D. |
为得到函数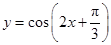 的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( )
A.向右平移 个长度单位 个长度单位 | B.向左平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
已知扇形的圆心角为2,半径为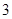 ,则扇形的面积是( )
,则扇形的面积是( )
| A.18 | B.6 | C.3 | D.9 |
函数 在一个周期内的图象如下,此函数的解析式为可为( ).
在一个周期内的图象如下,此函数的解析式为可为( ).
A. | B. |
C. | D. |
要得到函数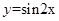 的图象,可以将
的图象,可以将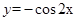 的图象( )
的图象( )
A.向左平移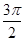 | B.向右平移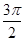 | C.向左平移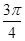 | D.向右平移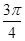 |
已知 ,并且
,并且 是第二象限的角,那么
是第二象限的角,那么 的值等于( )
的值等于( )
A. | B. | C. | D.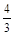 |
函数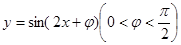 图象的一条对称轴在
图象的一条对称轴在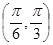 内,则满足此条件的一个
内,则满足此条件的一个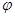 值为
值为
A.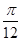 | B.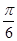 | C.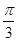 | D.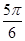 |
tan240°=
A. | B. | C.1 | D. |