题目内容
函数 (其中
(其中 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将
的图象,则只需将 的图象( )
的图象( )
A.向右平移 个长度单位 个长度单位 | B.向右平移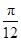 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向左平移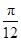 个长度单位 个长度单位 |
A
解析试题分析:由图像可知:函数 的周期为
的周期为 ,所以函数
,所以函数 在y轴左侧,与x轴的第一个交的坐标为
在y轴左侧,与x轴的第一个交的坐标为 ,所以为了得到
,所以为了得到 的图象,则只需将
的图象,则只需将 的图象向右平移
的图象向右平移 个长度单位。
个长度单位。
考点:函数 的解析式的求法;三角函数图像的变换。
的解析式的求法;三角函数图像的变换。
点评:此题可以不用求函数 的解析式,直接根据图像看平移。已知函数
的解析式,直接根据图像看平移。已知函数 的图像求解析式,是常见题型。一般的时候,(1)先求A;根据最值;(2)在求
的图像求解析式,是常见题型。一般的时候,(1)先求A;根据最值;(2)在求 :根据周期;(3)最后求
:根据周期;(3)最后求 :找到代入。
:找到代入。

练习册系列答案
相关题目
tan240°=
A. | B. | C.1 | D. |
已知 ,则点
,则点 位于( )
位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知 =
= ,0<x<π,则tanx为( )
,0<x<π,则tanx为( )
A.- | B.- | C.2 | D.-2 |
曲线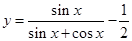 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )
A. | B. | C. | D. |
已知函数 (
( )的周期为
)的周期为 ,在一个周期内的图象如图所示,则正确的结论是( )
,在一个周期内的图象如图所示,则正确的结论是( )
A. | B. |
C. | D. |
点P 位于( )
位于( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
已知弧度数为2的圆心角所对的弦长也是2,则这个圆心角所对的弧长是
| A.2 | B. | C.2sin1 | D.sin2 |
 的图象向左平移
的图象向左平移 个单位, 再向上平移1个单位,所得图象的函数解析式是( ).
个单位, 再向上平移1个单位,所得图象的函数解析式是( ).


