题目内容
7．在数列{an}中，若a1=-2，an+1=an+n•2n，则an=（ ）| A． | （n-2）•2n | B． | 1-$\frac{1}{{2}^{n}}$ | C． | $\frac{2}{3}$（1-$\frac{1}{{4}^{n}}$） | D． | $\frac{2}{3}$（1-$\frac{1}{{2}^{n}}$） |
分析 利用累加法和错位相减法求数列的通项公式．
解答 解：∵an+1=an+n•2n，∴an+1-an=n•2n，
∴an-a1=an-an-1+an-1-an-2+…+a2-a1=（n-1）•2n-1+…+2•22+1•21，
∴2（an+2）=（n-1）•2n+（n-2）•2n-1+…+2•23+1•22，
∴-（an+2）=-（n-1）•2n+2n-1+2n-2+…+23+22+2=-（n-1）•2n+$\frac{2（1-{2}^{n-1}）}{1-2}$=-（n-1）•2n-2+2n，
∴an=（n-1）•2n+2-2n-2=（n-2）•2n，
故选：A．
点评 本题考查了数列递推式，训练了累加法和错位相减法求数列的通项公式，是中档题．
练习册系列答案
相关题目
15．若θ∈（0，π），且sinθ+cosθ=$\frac{1}{5}$，则曲线$\frac{{x}^{2}}{sinθ}$+$\frac{{y}^{2}}{cosθ}$=1是（ ）
| A． | 焦点在x轴上的椭圆 | B． | 焦点在y轴上的椭圆 | ||
| C． | 焦点在x轴上的双曲线 | D． | 焦点在y轴上的双曲线 |
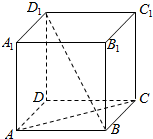如图，在棱长为2的正方体ABCD-A1B1C1D1中，过AC且与直线D1B平行的截面交D1D于点M，则△MAC的面积为=$\sqrt{6}$．