题目内容
3．
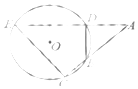如图，圆O的弦ED，CB的延长线交于点A．若BD⊥AE，AB=4，BC=2，AD=3，则DE= ；CE= ．（ ）| A． | 5、2$\sqrt{7}$ | B． | 5、7$\sqrt{7}$ | C． | 7 7$\sqrt{2}$ | D． | 5、$\sqrt{7}$ |
分析 首先根据题中圆的切线条件，依据割线定理求得一个线段AE的长，再根据勾股定理的线段的关系可求得CE的长度即可．
解答 解：首先由割线定，知道AB•AC=AD•AE，
于是AE=8，DE=5，又BD⊥AE，
故BE为直径，因此∠C=90°，
由勾股定理可知CE2=AE2-AC2=28，
故CE=2$\sqrt{7}$．
故选A．
点评 本题考查与圆有关的比例线段、平面几何的切割线定理，属容易题．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
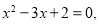则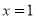 
”的逆否命题为：“若
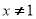, 则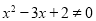
”．
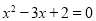”的充分不必要条件．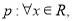
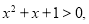则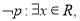
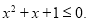
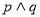为假命题，则
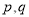均为假命题．
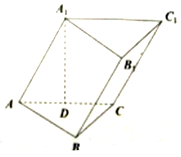如图，在斜三棱柱ABC-A1B1C1中，侧面ACC1A1是边长为4的菱形，BC⊥平面ACC1A1，CB=2，点A1在底面ABC上的射影D为棱AC的中点，点A在平面A1CB内的射影为E．
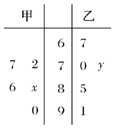某机械厂今年进行了五次技能考核，其中甲、乙两名技术骨干得分的平均分相等，成绩统计情况如茎叶图所示（其中a是0～9的某个整数）；