题目内容
16．已知向量$\overrightarrow{OA}$=（k，12），$\overrightarrow{OB}$=（4，5），$\overrightarrow{OC}$=（k，10），且A、B、C三点共线，则k=4．分析 利用向量共线定理即可得出．
解答 解：∵$\overrightarrow{AB}$=$\overrightarrow{OB}-\overrightarrow{OA}$=（4-k，-7），$\overrightarrow{BC}$=$\overrightarrow{OC}-\overrightarrow{OB}$=（k-4，5），A、B、C三点共线，
∴5（4-k）+7（k-4）=0，解得k=4．
故答案为：4．
点评 本题考查了向量共线定理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
,
，如果
，则
________
航空测量组的飞机航线和山顶在同一铅直平面内，已知飞机的高度为海拔10千米，速度为180千米/小时．飞机先看到山顶的俯角为15°，经过420秒后又看到山顶的俯角为45°，求山顶的海拔高度（取$\sqrt{2}=1.4$，$\sqrt{3}=1.7$）．
用部分自然构造如图的数表：用aij（i≥j）表示第i行第j个数（i，j∈N+），使得ai1=aii=i．每行中的其他各数分别等于其“肩膀”上的两个数之和．设第n（n∈N+）行的第二个数为bn（n≥2）．
3．
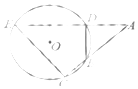如图，圆O的弦ED，CB的延长线交于点A．若BD⊥AE，AB=4，BC=2，AD=3，则DE= ；CE= ．（ ）
如图，圆O的弦ED，CB的延长线交于点A．若BD⊥AE，AB=4，BC=2，AD=3，则DE= ；CE= ．（ ）| A． | 5、2$\sqrt{7}$ | B． | 5、7$\sqrt{7}$ | C． | 7 7$\sqrt{2}$ | D． | 5、$\sqrt{7}$ |