题目内容
16．不等式（$\frac{1}{5}$）${\;}^{{x}^{2}-18}$＜5-3x的解集是（-∞，-3）∪（6，+∞）．分析 根据指数函数的单调性，得到x2-18＞3x，求出x的取值范围，写出不等式的解集．
解答 解：由（$\frac{1}{5}$）${\;}^{{x}^{2}-18}$＜5-3x=（$\frac{1}{5}$）3x，
得x2-18＞3x，
即x2-3x-18＞0，
即（x-6）（x+3）＞0，
解得x＜-3或x＞6，
故不等式的解集为（-∞，-3）∪（6，+∞），
故答案为：（-∞，-3）∪（6，+∞）．
点评 本题考查了指数函数的单调性和一元二次不等式的解法与应用问题，解题时应按照解一元二次不等式的基本步骤进行解答，是基础题．
练习册系列答案
相关题目
6．已知某随机变量X的概率密度函数P（x）满足P（x）=P（-x），当x≤0时，$P（x）=\frac{1}{2}{e^x}$，则随机变量X落在区间（-1，1）内的概率为（ ）
| A． | $1-\frac{1}{e}$ | B． | $\frac{e+1}{e^2}$ | C． | $\frac{1}{e}$ | D． | $\frac{e-1}{e^2}$ |
7．
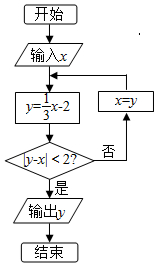执行如图所示的程序框图，若输入x=9，则输出的y的值为（ ）
执行如图所示的程序框图，若输入x=9，则输出的y的值为（ ）| A． | -$\frac{23}{9}$ | B． | 1 | C． | $\frac{8}{9}$ | D． | -$\frac{5}{3}$ |
4．已知集合M={x|-1≤x＜3}，集合$N=\left\{{x\left|{y=\sqrt{-{x^2}-x+6}}\right.}\right\}$，则M∪N=（ ）
| A． | M | B． | N | C． | {x|-1≤x≤2} | D． | {x|-3≤x＜3} |
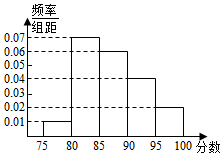2015年世界级体育盛会--世界田径锦标赛于8月22日下午在中国国家体育场鸟巢隆重开幕，在田径锦标赛期间需要大量大学生志愿者．志愿者先由相关的学校先进行选拔，合格者方能参加锦标赛组委会的面试．接到任务的某学校对报名的志愿者进行了一次相关知识小测试．现从中随机抽取100名学生的测试成绩，按成绩分组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，得到的频率分布直方图如图所示．
8．若x轴上一点A与点B（3，12）的距离等于13，则点A的坐标是（ ）
| A． | （-2，0）或（5，0） | B． | （8，9）或（10，0） | C． | （-2，0）或（8，0） | D． | （0，0）或（10，0） |
5．在等比数列{an}中，a1+a3=10，前4项和S4=30，则公比q等于（ ）
| A． | 3 | B． | $\frac{5}{2}$ | C． | 2 | D． | $\frac{3}{2}$ |