题目内容
(本小题满分13分)已知函数 是定义在
是定义在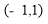 上的奇函数,且
上的奇函数,且 ,
,
(1)确定函数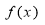 的解析式;
的解析式;
(2)用定义证明 在
在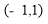 上是增函数;
上是增函数;
(3)解不等式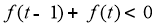 .
.
(1)
(2)见解析
(3)
【解析】
试题分析:本题主要考查的是有关奇函数的定义,解析式的求解,尤其注意奇函数中 的活用,用定义证明函数的单调性,应用函数的单调性,结合函数的定义域,解决有关函数不等式的求解问题,主要函数的定义域优先原则,即先保证函数的生存权.
的活用,用定义证明函数的单调性,应用函数的单调性,结合函数的定义域,解决有关函数不等式的求解问题,主要函数的定义域优先原则,即先保证函数的生存权.
试题解析:(1)依题意得 即
即 得
得
 --------4分
--------4分
(2)证明:任取 ,则
,则

 ,
,
又

∴ 在
在 上是增函数 ----9分
上是增函数 ----9分
(3)
 在
在 上是增函数,
上是增函数,
∴ ,解得
,解得 13分
13分
考点:奇函数图形过原点(0点有定义)的活用,用定义证明函数的单调性,应用函数的奇偶性和单调性转化函数不等式,将函数值的大小转化成自变量的大小关系,注意定义域优先原则.

练习册系列答案
相关题目
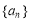 前
前 项和为
项和为 ,则下列一定成立的是
,则下列一定成立的是 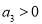 ,则
,则
 ,则
,则
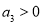 ,则
,则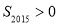
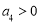 ,则
,则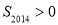
 ,
,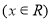 是一个以6为最小正周期的奇函数,则
是一个以6为最小正周期的奇函数,则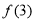 的值为( )
的值为( ) 和
和 分别是
分别是 上的偶函数和奇函数,则下列结论恒成立的是 ( )
上的偶函数和奇函数,则下列结论恒成立的是 ( ) 是奇函数
是奇函数  是奇函数
是奇函数 是偶函数
是偶函数  是偶函数
是偶函数
 ,若
,若 ,
, ,求实数
,求实数 的值.
的值. 是( )
是( ) ,
, __________。
__________。 如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.
如图,AB为圆O的直径,点E,F在圆O上,且AB∥EF,矩形ABCD所在的平面与圆O所在的平面互相垂直,且AB=2,AD=EF=1.