题目内容
7.已知数列{an}是等比数列,并且a1,a2+1,a3是公差为-3的等差数列.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=a2n,记Sn为数列{bn}的前n项和,证明:${S_n}<\frac{16}{3}$.
分析 (I)利用等差数列与等比数列的通项公式即可得出;
(II)利用等比数列的前n项和公式即可得出.
解答 (Ⅰ)解:设等比数列{an}的公比为q,
∵a1,a2+1,a3是公差为-3的等差数列,
∴$\left\{\begin{array}{l}{a_2}+1={a_1}-3\\{a_3}=({a_2}+1)-3\end{array}\right.$,
即$\left\{\begin{array}{l}{a_1}q-{a_1}=-4\\{a_1}{q^2}-{a_1}q=-2\end{array}\right.$,
解得${a_1}=8{,_{\;}}q=\frac{1}{2}$.
∴${a_n}={a_1}{q^{n-1}}=8×{(\frac{1}{2})^{n-1}}={2^{4-n}}$.
(Ⅱ)证明:∵$\frac{{{b_{n+1}}}}{b_n}=\frac{{{a_{2n+2}}}}{{{a_{2n}}}}=\frac{1}{4}$,
∴数列{bn}是以b1=a2=4为首项,$\frac{1}{4}$为公比的等比数列.
∴${S_n}=\frac{{4[1-{{(\frac{1}{4})}^n}]}}{{1-\frac{1}{4}}}$=$\frac{16}{3}[1-{(\frac{1}{4})^n}]<\frac{16}{3}$.
点评 本题考查了等差数列与等比数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.如图,在长方体ABCD-A1B1C1D1中,AA1=2AB,AB=BC,则下列结论中正确的是( )
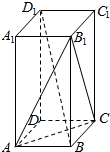

| A. | BD1∥B1C | B. | A1D1∥平面AB1C | C. | BD1⊥AC | D. | BD1⊥平面AB1C |
12.若向量 $\overrightarrow{a}$=($\sqrt{2}$,1),$\overrightarrow{b}$=(2,x)共线,则实数x的值是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 0 | D. | ±$\sqrt{2}$ |