题目内容
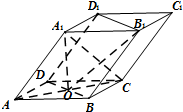如图，四棱柱ABCD-A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB=AA1=| 2 |
考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：由题意可得A1O为三棱柱ABD-A1B1D1的高，由勾股定理可得A1O=
的值，再根据三棱柱ABD-A1B1D1的体积V=S△ABD•A1O，运算求得结果．
| A1A2-AO2 |
解答：
解：由题意可得A1O为三棱柱ABD-A1B1D1的高．
三角形A1AO中，由勾股定理可得A1O=
=1，
∴三棱柱ABD-A1B1D1的体积V=S△ABD•A1O=
•A1O=1×1=1．
故答案为：1．
三角形A1AO中，由勾股定理可得A1O=
| A1A2-AO2 |
∴三棱柱ABD-A1B1D1的体积V=S△ABD•A1O=
| AB2 |
| 2 |
故答案为：1．
点评：本题主要考查棱柱的性质，考查三棱柱的体积，属于基础题．
练习册系列答案
相关题目
已知
=（2sin35°，2cos35°），
=（cos5°，-sin5°），则
•
=（ ）
| a |
| b |
| a |
| b |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、2sin40° |