题目内容
已知
=(2sin35°,2cos35°),
=(cos5°,-sin5°),则
•
=( )
| a |
| b |
| a |
| b |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、2sin40° |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积的坐标运算即可得出.
解答:
解:∵
=(2sin35°,2cos35°),
=(cos5°,-sin5°),
∴
•
=2sin35°cos5°-2cos35°sin5°=2sin(35°-5°)2sin30°=1.
故选:B.
| a |
| b |
∴
| a |
| b |
故选:B.
点评:本题考查了数量积的坐标运算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
cos(-240°)的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知y=sin30°,则导数y′=( )
A、
| ||||
B、-
| ||||
C、
| ||||
| D、0 |
下表是某厂1到4月份用水量情况(单位:百吨)的一组数据:
用水量y与月份x之间具有线性相关关系,其线性回归方程为
=-0.7x+a,则a的值为( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量ym3 | 4.5 | 4 | 3 | 2.5 |
| ∧ |
| y |
| A、5.25 | B、5 |
| C、2.5 | D、3.5 |
若数列{an}是等比数列,且an>0,则数列bn=
(n∈N*)也是等比数列.若数列{an}是等差数列,可类比得到关于等差数列的一个性质为( )
| n | a1a2•…•an |
A、bn=
| |||||
B、bn=
| |||||
C、bn=
| |||||
D、bn=
|
定义方程f(x)=f′(x)的实数根x0叫做f(x)的“新驻点”,若函数g(x)=x;h(x)=lnx;φ(x)=x3+1(0<x<2)的“新驻点”分别为α,β,γ,则( )
| A、β<α<γ |
| B、γ<β<α |
| C、γ<α<β |
| D、α<γ<β |
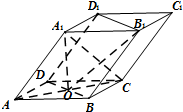 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=