题目内容
12.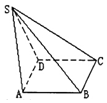 如图:ABCD是菱形,SAD是以AD为底边等腰三角形,$SA=SD=\sqrt{39}$,$AD=2\sqrt{3}$,且二面角S-AD-B大小为120°,∠DAB=60°.
如图:ABCD是菱形,SAD是以AD为底边等腰三角形,$SA=SD=\sqrt{39}$,$AD=2\sqrt{3}$,且二面角S-AD-B大小为120°,∠DAB=60°.(1)求证:AD⊥SB;
(2)求SC与SAD平面所成角的正弦值.
分析 (1)取AD的中点E,连SE,BE,证明AD⊥平面SBE,即可证明:AD⊥SB;
(2)过S作SO⊥直线BE,垂足为O,证明∠SEB为二面角的平面角,再求SC与SAD平面所成角的正弦值.
解答 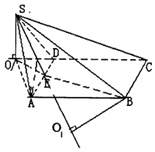 (1)证明:取AD的中点E,连SE,BE,
(1)证明:取AD的中点E,连SE,BE,
由题意知△ABD为正三角形,
∴SE⊥AD,BE⊥AD.
又SE∩BE=E,
∴AD⊥平面SBE,SB?平面SBE,
∴AD⊥SB.
(2)解:过S作SO⊥直线BE,垂足为O,
由(1)知平面ABCD⊥平面SBE,
则SO⊥平面ABCD,连OE,则AD⊥OE.
∴∠SEB为二面角的平面角,∠SEO=60°,
∴$SO=6sin60°=3\sqrt{3}$.
∵BC∥SAD,C到SAD距离为B到SAD距离,
由B作SE垂直BO1,由(1)知平面ASD⊥平面SBE,平面BO1⊥平面SAD,
BE=3,$B{O_1}=2sin60°=\frac{3}{2}\sqrt{3}$.OE=3,EB=3,∴OABD是平行四边形,O在直线CD上,SC2=SO2+OC2=27+48=75,$SC=5\sqrt{3}$.
设线面角为α,$sinα=\frac{{B{O_1}}}{SC}=\frac{3}{10}$,∴SC与平面SAD所成角的正弦值为$\frac{3}{10}$.
点评 本题考查线面垂直的判定与性质,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.设圆:x2+y2+2y-3=0与y轴交于A(0,y1),B(0,y2)两点,则y1y2 的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
7.设p:x2-x<1,$q:{log_2}({x^2}-x)<0$,则非p是非q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.某社区对社区内50名70岁以上老人的身体健康状况和对平时锻炼身体的积极性进行了调查,统计数据如表所示:
(1)如果在被调查的老人中随机抽查一名,那么抽到积极锻炼身体的老人的概率是多少?抽到不积极锻炼身体且健康状况一般的老人的概率是多少?
(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表)
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| 积极锻炼身体 | 不积极锻炼身体 | 合计 | |
| 健康状况良好 | 18 | 7 | 25 |
| 健康状况一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)试运用独立性检验思想方法判断能否有99%的把握说老人的身体健康状况与锻炼身体的积极性有关.(参考如表)
| P(k2>k) | 0.15 | 0.10 | 0.06 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
4.已知复数z=$\frac{(-1+i)(2+i)}{-i}$,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.执行如图的程序框图,如果输入的x∈[-1,3],输出的y∈[0,4],则输入的a的取值范围为( )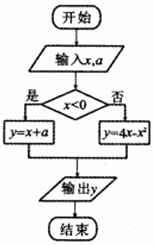

| A. | [-3,4] | B. | [1,4] | C. | [-3,0] | D. | [0,1] |