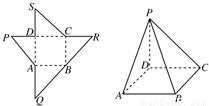
题目内容
 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要________个这样的几何体,可以拼成一个棱长为6的正方体.
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要________个这样的几何体,可以拼成一个棱长为6的正方体.
3
分析:将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD,求出棱锥的体积,正方体的体积,然后确定几何体的个数.
解答:由题意知,将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD(如图),其中PD⊥平面ABCD,因此该四棱锥的体积V= ×6×6×6=72,而棱长为6的正方体的体积V=6×6×6=216,故需要
×6×6×6=72,而棱长为6的正方体的体积V=6×6×6=216,故需要 =3个这样的几何体,才能拼成一个棱长为6的正方体.
=3个这样的几何体,才能拼成一个棱长为6的正方体.
故答案为:3
点评:本题是基础题,考查棱锥的体积,资费通的体积的求法,考查折叠问题,空间想象能力,计算能力.
分析:将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD,求出棱锥的体积,正方体的体积,然后确定几何体的个数.
解答:由题意知,将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD(如图),其中PD⊥平面ABCD,因此该四棱锥的体积V=
 ×6×6×6=72,而棱长为6的正方体的体积V=6×6×6=216,故需要
×6×6×6=72,而棱长为6的正方体的体积V=6×6×6=216,故需要 =3个这样的几何体,才能拼成一个棱长为6的正方体.
=3个这样的几何体,才能拼成一个棱长为6的正方体.
故答案为:3
点评:本题是基础题,考查棱锥的体积,资费通的体积的求法,考查折叠问题,空间想象能力,计算能力.

练习册系列答案
相关题目
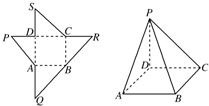 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要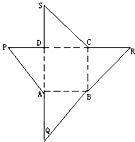 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则该几何体的内切球的半径为
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则该几何体的内切球的半径为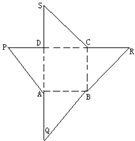 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠,使P,Q,R,S四点重合,则需要
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠,使P,Q,R,S四点重合,则需要