题目内容
3.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2}$)的图象如图所示,则A+ω+φ=( )
| A. | $2+\frac{π}{6}$ | B. | $2+\frac{π}{3}$ | C. | $4+\frac{π}{6}$ | D. | $4+\frac{π}{3}$ |
分析 根据函数f(x)的图象与性质,求出周期T与ω的值;图象过($\frac{2}{3}π$,-2)代入求解φ,即可求A+ω+φ的值.
解答 解:从图象信息可知,A=$\frac{2-(-2)}{2}=2$,
周期T=2×($\frac{2π}{3}-\frac{π}{6}$)=π
∴ω=$\frac{2π}{T}=2$.
∵图象过($\frac{2}{3}π$,-2),
∴-2=2sin(2×$\frac{2π}{3}$+φ),即sin($\frac{4π}{3}$+φ)=-1.
∵$|φ|<\frac{π}{2}$)
∴φ=$\frac{π}{6}$.
则A+ω+φ=2+2+$\frac{π}{6}$=4+$\frac{π}{6}$.
故选:C.
点评 本题考查了三角函数的图象与性质的应用问题,能根据图象信息求解解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知某几何体的三视图如图所示,则该几何体的体积是( )


| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
18.如果执行如图的框图,则输出的数S=( )
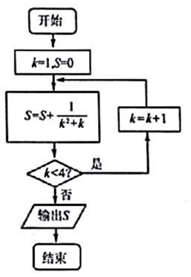

| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{5}{6}$ |
15.过点P(4,3),且斜率为$\frac{2}{3}$的直线的参数方程为( )
| A. | $\left\{\begin{array}{l}{x=4+\frac{3}{\sqrt{13}}t}\\{y=3+\frac{2}{\sqrt{13}}t}\end{array}\right.$(t为参数) | B. | $\left\{\begin{array}{l}{x=3+\frac{3}{\sqrt{13}}t}\\{y=4+\frac{2}{\sqrt{13}}t}\end{array}\right.$(t为参数) | ||
| C. | $\left\{\begin{array}{l}{x=4+\frac{2}{\sqrt{13}}t}\\{y=3+\frac{3}{\sqrt{13}}t}\end{array}\right.$(t为参数) | D. | $\left\{\begin{array}{l}{x=3+\frac{2}{\sqrt{13}}t}\\{y=4+\frac{3}{\sqrt{13}}t}\end{array}\right.$(t为参数) |
5.已知集合A={α|α=k•360°,k∈Z},集合B={α|α=k•180°,k∈Z},集合C={α|α=k•90°,k∈Z},则下列关系中正确的是( )
| A. | A=B=C | B. | A=(B∩C) | C. | (A∪B)=C | D. | A?B?C |
