题目内容
(本小题满分14分)已知正三角形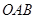 的三个顶点都在抛物线
的三个顶点都在抛物线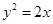 上,其中
上,其中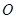 为坐标原点,设圆
为坐标原点,设圆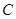 是
是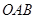 的内接圆(点
的内接圆(点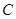 为圆心)
为圆心)
(I)求圆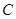 的方程;
的方程;
(II)设圆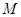 的方程为
的方程为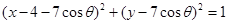 ,过圆
,过圆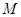 上任意一点
上任意一点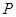 分别作圆
分别作圆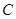 的两条切线
的两条切线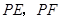 ,切点为
,切点为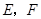 ,求
,求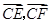 的最大值和最小值.
的最大值和最小值.
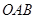 的三个顶点都在抛物线
的三个顶点都在抛物线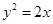 上,其中
上,其中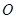 为坐标原点,设圆
为坐标原点,设圆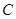 是
是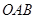 的内接圆(点
的内接圆(点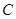 为圆心)
为圆心)(I)求圆
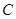 的方程;
的方程;(II)设圆
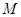 的方程为
的方程为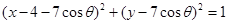 ,过圆
,过圆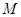 上任意一点
上任意一点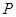 分别作圆
分别作圆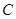 的两条切线
的两条切线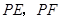 ,切点为
,切点为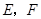 ,求
,求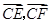 的最大值和最小值.
的最大值和最小值.(I)圆C的方程为
(II) 的最大值为
的最大值为 ,最小值为
,最小值为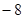

(II)
 的最大值为
的最大值为 ,最小值为
,最小值为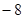
解法一:设A、B两点坐标分别为 ,由题设知
,由题设知
 解得
解得
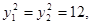
所以
设圆心C的坐标为(r,0),则 因此圆C的方程为
因此圆C的方程为
 4分
4分
解法二:设A、B两点坐标分别为 由题设知
由题设知
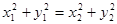 .
.
又因为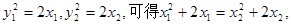 即
即
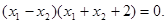
由x1>0,x2>0,可知x1=x2,故A、B两点关于x轴对称,所以圆心C在x轴上.
设C点的坐标为(r,0),则A点坐标为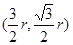 ,于是有
,于是有 ,解得r=4,所以圆C的方程为
,解得r=4,所以圆C的方程为
 4分
4分
(Ⅱ)解:设∠ECF=2a,则
 . 8分
. 8分
在Rt△PCE中, .由圆的几何性质得
.由圆的几何性质得
 ≤
≤
 ≥
≥ 10分
10分
所以 ≤
≤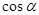 ≤
≤ ,由此可得
,由此可得
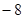 ≤
≤ ≤
≤ .
.
故 的最大值为
的最大值为 ,最小值为
,最小值为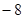 . 14分
. 14分
 ,由题设知
,由题设知 解得
解得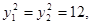
所以

设圆心C的坐标为(r,0),则
 因此圆C的方程为
因此圆C的方程为 4分
4分解法二:设A、B两点坐标分别为
 由题设知
由题设知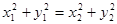 .
.又因为
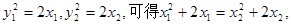 即
即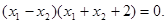
由x1>0,x2>0,可知x1=x2,故A、B两点关于x轴对称,所以圆心C在x轴上.
设C点的坐标为(r,0),则A点坐标为
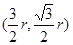 ,于是有
,于是有 ,解得r=4,所以圆C的方程为
,解得r=4,所以圆C的方程为 4分
4分(Ⅱ)解:设∠ECF=2a,则
 . 8分
. 8分在Rt△PCE中,
 .由圆的几何性质得
.由圆的几何性质得 ≤
≤
 ≥
≥ 10分
10分所以
 ≤
≤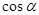 ≤
≤ ,由此可得
,由此可得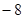 ≤
≤ ≤
≤ .
.故
 的最大值为
的最大值为 ,最小值为
,最小值为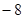 . 14分
. 14分
练习册系列答案
相关题目
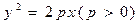 的对称轴上一点
的对称轴上一点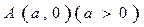 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线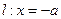 作垂线,垂足分别为
作垂线,垂足分别为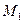 、
、 。
。 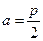 时,求证:
时,求证: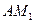 ⊥
⊥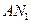 ;
;
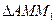 、
、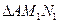 、
、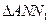 的面积分别为
的面积分别为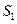 、
、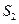 、
、 ,是否存在
,是否存在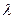 ,使得对任意的
,使得对任意的 ,都有
,都有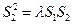 成立。若存在,求
成立。若存在,求 点.
点.  边形BB1D1D的面积,求
边形BB1D1D的面积,求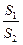 的取值范围.
的取值范围.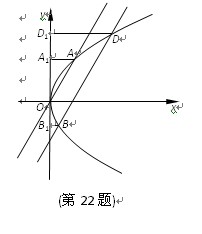
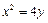 上一点
上一点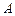 的纵坐标为4,则点
的纵坐标为4,则点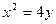 的焦点为F,
的焦点为F,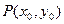 为抛物线上的任一点(其中
为抛物线上的任一点(其中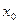 ≠0),[
≠0),[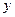 轴于Q点.
轴于Q点.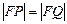 ;
;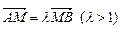 ,求
,求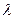 的值.
的值.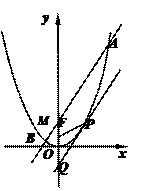
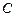 :
: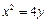 的焦点为
的焦点为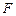 ,过点
,过点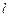 交抛物线
交抛物线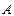 、
、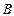 两点;椭圆
两点;椭圆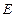 的中心在原点,焦点在
的中心在原点,焦点在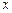 轴上,点
轴上,点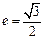 .
.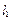 、
、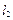 ,切线
,切线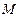 .证明:
.证明: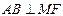 ;
;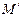 ,经过点
,经过点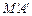 、
、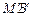 (
(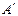 、
、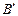 为切点),使得直线
为切点),使得直线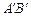 过点
过点
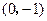 的直线l与抛物线
的直线l与抛物线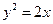 有且只有一个交点,则这样的直线l共有 条. [答]( )
有且只有一个交点,则这样的直线l共有 条. [答]( )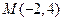 和抛物线
和抛物线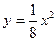 的焦点F,在抛物线上求一点P使|PM|+|PF|的值最小,则
的焦点F,在抛物线上求一点P使|PM|+|PF|的值最小,则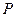 点的坐标是
点的坐标是 。
。 焦点F的直线
焦点F的直线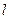 与它相交于A、B两点,则弦AB的中点的轨迹方程是 。
与它相交于A、B两点,则弦AB的中点的轨迹方程是 。