题目内容
(本小题满分15分)
如图,设抛物线C: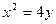 的焦点为F,
的焦点为F,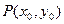 为抛物线上的任一点(其中
为抛物线上的任一点(其中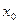 ≠0),[
≠0),[
过P点的切线交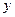 轴于Q点.
轴于Q点.
(Ⅰ)证明: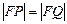 ;
;
(Ⅱ)Q点关于原点O的对称点为M,过M点作平行于PQ的直线
交抛物线C于A、B两点,若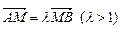 ,求
,求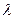 的值.
的值.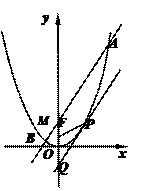
如图,设抛物线C:
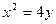 的焦点为F,
的焦点为F,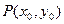 为抛物线上的任一点(其中
为抛物线上的任一点(其中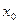 ≠0),[
≠0),[过P点的切线交
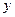 轴于Q点.
轴于Q点.(Ⅰ)证明:
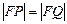 ;
;(Ⅱ)Q点关于原点O的对称点为M,过M点作平行于PQ的直线
交抛物线C于A、B两点,若
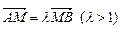 ,求
,求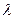 的值.
的值.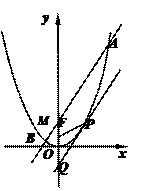
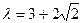
(Ⅰ)证明:由抛物线定义知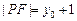 ,
,
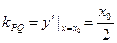 ,
,
可得PQ所在直线方程为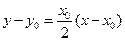 ,
,
∵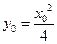
∴得Q点坐标为(0,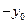 )
)
∴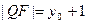 ∴ |PF|=|QF|
∴ |PF|=|QF|
(Ⅱ)设A(x1, y1),B(x2, y2),又M点坐标为(0, y0)
∴AB方程为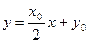 …….8分。
…….8分。
由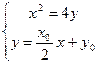 得
得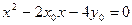
∴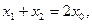
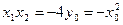 ……① …….10分。
……① …….10分。
由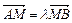 得:
得: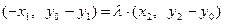 ,
,
∴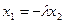 ……② …….12分。
……② …….12分。
由①②知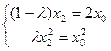 ,得
,得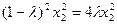 ,由x0≠0可得x2≠0,
,由x0≠0可得x2≠0,
∴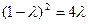 ,又
,又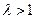 ,解得:
,解得: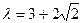 . …….15分。
. …….15分。
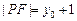 ,
, 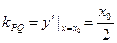 ,
,可得PQ所在直线方程为
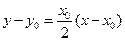 ,
,∵
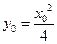
∴得Q点坐标为(0,
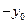 )
) ∴
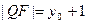 ∴ |PF|=|QF|
∴ |PF|=|QF| (Ⅱ)设A(x1, y1),B(x2, y2),又M点坐标为(0, y0)
∴AB方程为
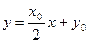 …….8分。
…….8分。由
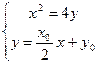 得
得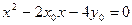
∴
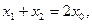
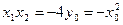 ……① …….10分。
……① …….10分。由
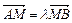 得:
得: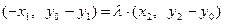 ,
, ∴
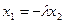 ……② …….12分。
……② …….12分。由①②知
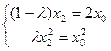 ,得
,得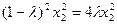 ,由x0≠0可得x2≠0,
,由x0≠0可得x2≠0,∴
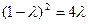 ,又
,又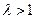 ,解得:
,解得: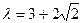 . …….15分。
. …….15分。 

练习册系列答案
相关题目
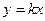 分抛物线
分抛物线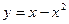 与
与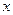 轴所围成图形为面积相等的两个部分,则
轴所围成图形为面积相等的两个部分,则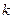 的值 .
的值 .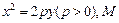 直线
直线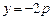 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。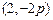 时,
时,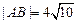 ,求此时抛物线的方程;
,求此时抛物线的方程;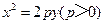 上,其中,点C满足
上,其中,点C满足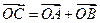 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.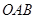 的三个顶点都在抛物线
的三个顶点都在抛物线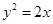 上,其中
上,其中 为坐标原点,设圆
为坐标原点,设圆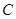 是
是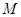 的方程为
的方程为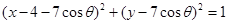 ,过圆
,过圆 分别作圆
分别作圆 ,切点为
,切点为 ,求
,求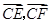 的最大值和最小值.
的最大值和最小值. 已知抛物线
已知抛物线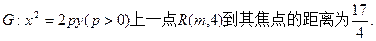
 为—1的直线l交抛物线G于另一点A,交x轴于点B,若|OA|=|OB|(O为坐标原点),求点P的坐标。
为—1的直线l交抛物线G于另一点A,交x轴于点B,若|OA|=|OB|(O为坐标原点),求点P的坐标。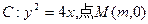 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线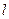 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。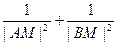 恒为定值。
恒为定值。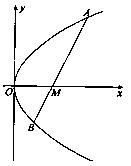
 是抛物线
是抛物线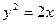 上的一个动点,则点
上的一个动点,则点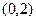 的距离与
的距离与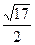
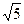
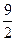
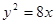 上一点
上一点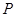 到其焦点的距离为
到其焦点的距离为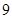 ,则点
,则点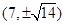
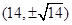
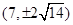
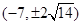
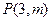 在以点
在以点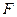 为焦点的抛物线
为焦点的抛物线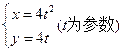 上,则
上,则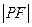 等于 .
等于 .