题目内容
求函数y=ln
的值域.
| 2+x |
| 2-x |
考点:对数函数的值域与最值
专题:函数的性质及应用
分析:根据f(-x)=ln
=-ln
=-f(x),f(x)=ln
=ln(
-1)单调递增,运用复合函数的性质求解.
| 2-x |
| 2+x |
| 2+x |
| 2-x |
| 2+x |
| 2-x |
| 4 |
| 2-x |
解答:
解:∵函数f(x)=ln
,
∴f(-x)=ln
=-ln
=-f(x),
∴f(x)是奇函数,∵
>0,即x∈(-2,2)
∵f(x)=ln
=ln(
-1)单调递增,
∴函数y=ln
的值域(-∞,+∞)
| 2+x |
| 2-x |
∴f(-x)=ln
| 2-x |
| 2+x |
| 2+x |
| 2-x |
∴f(x)是奇函数,∵
| 2+x |
| 2-x |
∵f(x)=ln
| 2+x |
| 2-x |
| 4 |
| 2-x |
∴函数y=ln
| 2+x |
| 2-x |
点评:本题考查了函数的单调性,奇偶性,属于中档题,

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
已知函数y=2015cos(ωx+φ)(ω>0,0<φ<π),满足f(-x)=-f(x),其图象与直线y=0的某两个交点的横坐标分别为x1,x2,|x1-x2|的最小值为π,则( )
A、ω=2,φ=
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=
| ||
D、ω=1,φ=
|
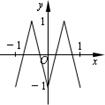
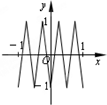
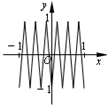
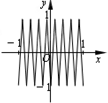
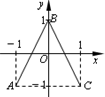 如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )
如图,函数y=f(x)的图象为折线ABC,设f1(x)=f(x),fn+1(x)=fn(x),n∈N,则函数f4(x)的图象为( )